Hostname: page-component-669899f699-ggqkh Total loading time: 0 Render date: 2025-04-29T13:52:39.508Z Has data issue: false hasContentIssue false
  • English
  • Français

Separating H-sets by Open Sets

Published online by Cambridge University Press:  20 November 2018

Jack Porter  and
Mohan Tikoo
Jack Porter
Affiliation:
Department of Mathematics, University of Kansas, Lawrence, KS 66045, USA e-mail: [email protected]
Mohan Tikoo
Affiliation:
Department of Mathematics, Southeast Missouri State University, Cape Girardeau, MO 63701, USA e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In an 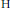$\text{H}$-closed, Urysohn space, disjoint 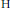$\text{H}$-sets can be separated by disjoint open sets. This is not true for an arbitrary H-closed space even if one of the 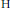$\text{H}$-sets is a point. In this paper, we provide a systematic study of those spaces in which disjoint 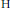$\text{H}$-sets can be separated by disjoint open sets.

Keywords

54C0854D1054D15H-setH-closed0-continuous
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 2 , 01 June 2010 , pp. 360 - 366
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Alexandroff, P. S. and Urysohn, P., Zur Theorie der topologischen Räume. Math. Ann. 92, 1924, no. 3-4, 258–266. doi:10.1007/BF01448008Google Scholar
[2] Dickman, R. F. Jr. and Porter, J. R., θ-closed subsets of Hausdorff spaces. Pacific. J. Math. 59(1975), no. 2, 407–415.Google Scholar
[3] Dickman, R. F. Jr. Porter, J. R., and Rubin, L. R., Completely regular absolutes and projective objects. Pacific. J. Math. 94(1981), no. 2, 277–295.Google Scholar
[4] Fomin, S. Extensions of topological spaces. Ann. of Math. 44(1943), 471–480. doi:10.2307/1968976Google Scholar
[5] Hodel, R. E., A theory of convergence and cluster points based on κ-nets. Top. Proc. 35(2010), 291–330.Google Scholar
[6] Iliadis, S., Absolutes of Hausdorff spaces Dokl. Akad. Nauk. SSSR 149(1963)22–25.Google Scholar
[7] Porter, J. and Tikoo, M., On Katětov spaces. Canad. Math. Bull. 32(1989), no. 4, 425–433.Google Scholar
[8] Porter, J. and Votaw, C., S(α) spaces and regular Hausdorff extensions. Pacific J. Math 45(1973), 327–345.Google Scholar
[9] Porter, J. and Woods, G., Extensions and Absolutes of Hausdorff Spaces. Springer-Verlag, New York, 1988.Google Scholar
[10] Tikoo, M., A note on H-sets. Kyungpook Math. J. 28(1988), no. 1, 91–95.Google Scholar
[11] Veličko, N. V., H-closed topological spaces. Amer. Math. Soc. Transl. 78(1968), 103– 118.Google Scholar
[12] Vermeer, J., Closed spaces of H-closed spaces. Pacific J. Math. 118(1985), no. 1, 229–247.Google Scholar