Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-30T19:10:26.262Z Has data issue: false hasContentIssue false
  • English
  • Français

Retract Rationality and Algebraic Tori

Part of: Linear algebraic groups and related topics Forms and linear algebraic groups Representation theory of groups Birational geometry

Published online by Cambridge University Press:  18 July 2019

Federico Scavia
Federico Scavia*
Affiliation:
University of British Columbia, Vancouver, BC V6T1Z4 Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For any prime number 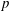$p$ and field 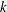$k$, we characterize the 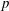$p$-retract rationality of an algebraic 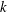$k$-torus in terms of its character lattice. We show that a 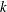$k$-torus is retract rational if and only if it is 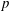$p$-retract rational for every prime 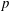$p$, and that the Noether problem for retract rationality for a group of multiplicative type 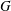$G$ has an affirmative answer for 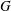$G$ if and only if the Noether problem for 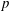$p$-retract rationality for 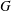$G$ has a positive answer for all 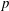$p$. For every finite set of primes 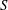$S$ we give examples of tori that are 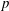$p$-retract rational if and only if 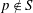$p\notin S$.

Keywords

algebraic toriretract rationalityNoether probleminvertible lattice

MSC classification

Primary: 11E72: Galois cohomology of linear algebraic groups
Secondary: 14E08: Rationality questions 20C10: Integral representations of finite groups 20G15: Linear algebraic groups over arbitrary fields
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 1 , March 2020 , pp. 173 - 186
Copyright
© Canadian Mathematical Society 2019

References

Artin, M. and Mumford, D., Some elementary examples of unirational varieties which are not rational. Proc. London Math. Soc. 3(1972), no. 1, 75–95. https://doi.org/10.1112/plms/s3-25.1.75.Google Scholar
Beauville, A., Colliot-Thélène, J.-L., Sansuc, J.-J., and Swinnerton-Dyer, P., Variétés stablement rationnelles non rationnelles. Ann. of Math. (2) 121(1985), no. 2, 283–318. https://doi.org/10.2307/1971174.Google Scholar
Brown, K. S., Cohomology of groups. Graduate Texts in Mathematics, 87, Springer-Verlag, New York, 1994. Corrected reprint of the 1982 original.Google Scholar
Clemens, C. H. and Griffiths, P. A., The intermediate Jacobian of the cubic threefold. Ann. of Math. 95(1972), 281–356. https://doi.org/10.2307/1970801.Google Scholar
Colliot-Thélène, J.-L. and Pirutka, A., Hypersurfaces quartiques de dimension 3: non-rationalité stable. Ann. Sci. Éc. Norm. Supér. (4) 49(2016), no. 2, 371–397. https://doi.org/10.24033/asens.2285.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., La R-équivalence sur les tores. Ann. Sci. Éc. Norm. Supér. 10(1977), 175–229.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., Principal homogeneous spaces under flasque tori: applications. J. Algebra 106(1987), 148–205. https://doi.org/10.1016/0021-8693(87)90026-3.Google Scholar
Colliot-Thélène, J.-L. and Sansuc, J.-J., The rationality problem for fields of invariants under linear algebraic groups (with special regards to the Brauer group). In: Algebraic groups and homogeneous spaces. Tata Inst. Fund. Res. Stud. Math., 19, Tata Inst. Fund. Res., Mumbai, 2007, pp. 113–186.Google Scholar
Endô, S. and Miyata, T., Invariants of finite abelian groups. J. Math. Soc. Japan 2(1973), 7–26. https://doi.org/10.2969/jmsj/02510007.Google Scholar
Endô, S. and Miyata, T., On a classification of the function fields of algebraic tori. Nagoya Math. J. 5(1975), 85–104.Google Scholar
Florence, M. and Reichstein, Z., The rationality problem for forms of M 0, n. Bull. London Math. Soc. 50(2018), 148–158. https://doi.org/10.1112/blms.12126.Google Scholar
Iskovskih, V. A. and Manin, J. I., Three-dimensional quartics and counterexamples to the Lüroth problem. Math. SB 86(128)(1971), 140–166.Google Scholar
Kunyavskiĭ, B. È., Tori with a biquadratic splitting field. Izv. Akad. Nauk SSSR Ser. Mat. 42(1978), no. 3, 580–587.Google Scholar
Kunyavskiĭ, B. È., Three-dimensional algebraic tori. In: Investigations in number theory (Russian). Saratov. Gos. Univ., Saratov, 1987, pp. 90–111. Translated in Selecta Math. Soviet. 9(1990), no. 1, 1–21.Google Scholar
Lang, S., Algebra. Graduate Texts in Mathematics, 211, Springer-Verlag, New York, 2002. https://doi.org/10.1007/978-1-4613-0041-0.Google Scholar
Lorenz, M., Multiplicative invariant theory. Encyclopaedia of Mathematical Sciences, 135, Springer-Verlag, Berlin, 2006.Google Scholar
Maeda, T., Noether’s problem for A 5. J. Algebra 125(1989), 418–430. https://doi.org/10.1016/0021-8693(89)90174-9.Google Scholar
Merkurjev, A. S., Versal torsors and retracts. http://www.math.ucla.edu/∼merkurev/publicat.htm, 2018.Google Scholar
Miyata, T., Invariants of certain groups. I. Nagoya Math. J. 41(1971), 69–73.Google Scholar
Ohm, J., On subfields of rational function fields. Arch. Math. (Basel) 42(1984), no. 2, 136–138. https://doi.org/10.1007/BF01772932.Google Scholar
Reichstein, Z. and Vistoli, A., Birational isomorphisms between twisted group actions. J. Lie Theory 16(2006), no. 4, 791–802.Google Scholar
Roquette, P., Isomorphisms of generic splitting fields of simple algebras. J. Reine Angew. Math. 214/215(1964), 207–226. https://doi.org/10.1515/crll.1964.214-215.207.Google Scholar
Saltman, D. J., Generic structures and field theory. Algebraists Hommage, 1982.Google Scholar
Saltman, D. J., Retract rational fields and cyclic Galois extensions. Israel J. Math. 47(1984), no. 2–3, 165–215. https://doi.org/10.1007/BF02760515.Google Scholar
Schreieder, S., Stably irrational hypersurfaces of small slopes. arxiv:1801.05397.Google Scholar
Totaro, B., Hypersurfaces that are not stably rational. J. Amer. Math. Soc. 29(2016), no. 3, 883–891. https://doi.org/10.1090/jams/840.Google Scholar
Voisin, C., Unirational threefolds with no universal codimension 2 cycle. Invent. Math. 201(2015), no. 1, 207–237. https://doi.org/10.1007/s00222-014-0551-y.Google Scholar
Voskresenskiĭ, V. E., Algebraic groups and their birational invariants, Translated from the Russian manuscript by Boris È. Kunyavskiĭ. Translations of Mathematical Monographs, 179. American Mathematical Society, Providence, RI, 1998.Google Scholar
Voskresenskiĭ, V. E., On two-dimensional algebraic tori. Izv. Akad. Nauk SSSR Ser. Mat. 29(1965), 239–244.Google Scholar
Voskresenskiĭ, V. E., Rationality of certain algebraic tori. Izv. Akad. Nauk SSSR Ser. Mat. 35(1971), 1037–1046.Google Scholar
Voskresenskiĭ, V. E., Fields of invariants of abelian groups. Uspehi Mat. Nauk 28(1973), no. 4(172), 77–102.Google Scholar