Published online by Cambridge University Press: 20 November 2018
Let 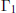 ${{\Gamma }_{1}}$ and
${{\Gamma }_{1}}$ and 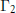 ${{\Gamma }_{2}}$ be Bieberbach groups contained in the full isometry group
${{\Gamma }_{2}}$ be Bieberbach groups contained in the full isometry group  $G$ of
$G$ of  ${{\mathbb{R}}^{n}}$. We prove that if the compact flat manifolds
${{\mathbb{R}}^{n}}$. We prove that if the compact flat manifolds 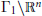 ${{\Gamma }_{1}}\backslash {{\mathbb{R}}^{n}}$ and
${{\Gamma }_{1}}\backslash {{\mathbb{R}}^{n}}$ and 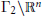 ${{\Gamma }_{2}}\backslash {{\mathbb{R}}^{n}}$ are strongly isospectral, then the Bieberbach groups
${{\Gamma }_{2}}\backslash {{\mathbb{R}}^{n}}$ are strongly isospectral, then the Bieberbach groups 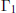 ${{\Gamma }_{1}}$ and
${{\Gamma }_{1}}$ and 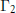 ${{\Gamma }_{2}}$ are representation equivalent; that is, the right regular representations
${{\Gamma }_{2}}$ are representation equivalent; that is, the right regular representations 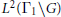 ${{L}^{2}}\left( {{\Gamma }_{1}}\backslash G \right)$ and
${{L}^{2}}\left( {{\Gamma }_{1}}\backslash G \right)$ and 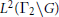 ${{L}^{2}}\left( {{\Gamma }_{2}}\backslash G \right)$ are unitarily equivalent.
${{L}^{2}}\left( {{\Gamma }_{2}}\backslash G \right)$ are unitarily equivalent.
Supported by CONICET and Secyt-UNC