Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-26T15:04:59.841Z Has data issue: false hasContentIssue false
  • English
  • Français

Reduction to Dimension Two of the Local Spectrum for an AH Algebra with the Ideal Property

Published online by Cambridge University Press:  20 November 2018

Chunlan Jiang
Chunlan Jiang*
Affiliation:
Department of Mathematics, Hebei Normal University, Shijiazhuang, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A 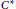${{C}^{*}}$-algebra Ahas the ideal property if any ideal $I$ of 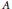$A$ is generated as a closed two-sided ideal by the projections inside the ideal. Suppose that the limit 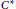${{C}^{*}}$-algebra 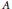$A$ of inductive limit of direct sums of matrix algebras over spaces with uniformly bounded dimension has the ideal property. In this paper we will prove that 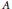$A$ can be written as an inductive limit of certain very special subhomogeneous algebras, namely, direct sum of dimension-drop interval algebras and matrix algebras over 2-dimensional spaces with torsion 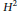${{H}^{2}}$ groups.

Keywords

46L35AH algebrareductionlocal spectrumideal property
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 60 , Issue 4 , 01 December 2017 , pp. 791 - 806
Copyright
Copyright © Canadian Mathematical Society 2017

References

[Bla] Blackadar, B., Matricial and ultra-matricial topology. In: Operator algebras, physics, and low-dimensional topology (Istanbul, 1991), Res. Notes Math.,! Wellesley, MA, 1993, pp. 11–38 Google Scholar
[Dl] Dadarlat, M., Approximately unitarily equivalent, morphisms and inductive Jf-theory 9(1995), 117–137. http://dx.doi.org/10.1007/BF00961456 Google Scholar
[D2] Dadarlat, M., Reduction to dimension three of local spectra of Real rank zero C*-c Angew. Math. 460(1995), 189–212. http://dx.doi.org/10.1 51 5/crll.1 995.460.11 Google Scholar
[DG] Dadarlat, M. and G. Gong, A classification result for approximately homoger, of real rank zero. Geom. Funct. Anal. 7(1997), no. 4, 646–711. http://dx.doi.org/10.1007/s000390050023 Google Scholar
[DN] Dadarlat, M. and A. Nemethi, Sharp theory and (connective) K-theory. J. OfGoogle Scholar
[Bla] Blackadar, B., Matricial and ultra-matricial topology. In: Operator algebras, mathematical physics, and low-dimensional topology (Istanbul, 1991), Res. Notes Math., 54, A K Peter, Wellesley, MA, 1993, pp. 11–38 Google Scholar
[Dl] Dadarlat, M., Approximately unitarily equivalent, morphisms and inductive limit C* -algebras. Jf-theory 9(1995), 117–137. http://dx.doi.org/10.1007/BF00961456 Google Scholar
[D2] Dadarlat, M., Reduction to dimension three of local spectra of Real rank zero C* -algebras. J. Reine Angew. Math. 460(1995), 189–212. http://dx.doi.org/10.1 51 5/crll.1 995.460.1 89 Google Scholar
[DG] Dadarlat, M. and G. Gong, A classification result for approximately homogeneous C* -algebras of real rank zero. Geom. Funct. Anal. 7(1997), no. 4, 646–711. http://dx.doi.org/10.1007/s000390050023 Google Scholar
[DN] Dadarlat, M. and A. Nemethi, Sharp theory and (connective) K-theory. J. Operator Theory 23(1990), no. 2, 207–291.Google Scholar
[Elll] Elliott, G. A., On the classification of C* -algebras of real rank zero. J. Reine Angew. Math. 443(1993), 179–219. http://dx.doi.org/10.1515/crll.1993.443.179 Google Scholar
[E112] Elliott, G. A., A classification of certain simple C* -algebras. In: Quantum and non-commutative analysis (Kyoto, 1992), Math. Phys. Stud., 16, Kluwer, Dordrecht, 1993, pp. 373–385.Google Scholar
[E113] Elliott, G. A., A classification of certain simple C* -algebras. II. J. Ramanujan Math. Soc. 12(1997), no. 1, 97–134.Google Scholar
[EG1] Elliott, G. A. and G. Gong, On the inductive limits of matrix algebras over two-tori. Amer. J. Math 118(1996), no. 2, 263–290.Google Scholar
[EG2] Elliott, G. A., On the classification of C* -algebras of real rank zero. II. Ann. of Math 144(1996), no. 3, 497–610. http://dx.doi.org/1 0.2307/211 8565 Google Scholar
[EGL1] Elliott, G. A., G. Gong, and L. Li, On the classification of simple inductive limit C* -algebras. II. The isomorphism theorem. Invent. Math. 168(2007), no. 2, 249–320. http://dx.doi.org/10.1007/s00222-006-0033-y Google Scholar
[EGL2] Elliott, G. A., Injectivity of the connecting maps in AH inductive limit systems. C. R. Math. Acad. Sci. Soc. R. Can. 26(2004), no. 1, 4–10.Google Scholar
[EGS] Elliott, G. A., G. Gong, and H. Su, On the classification of C* -algebras of real rank zero. IV. Reduction to local spectrum of dimension two. In: Operator algebras and their applications, II (Waterloo, ON, 1994/1995), Fields Inst. Commun., 20, American Mathematical Society, Providence, RI, 1998, pp. 73–95.Google Scholar
[Gl] Gong, G., Approximation by dimension drop C* -algebras and classification. C. R. Math. Rep. Acad. Sci Can. 16(1994), no. 1, 40–44.Google Scholar
[G2] Gong, G., Classification of C*-algebras of real rank zero and unsuspended E-equivalence types. J. Funct. Anal. 152(1998), 281–329. http://dx.doi.org/10.1006/jfan.1997.3165, Google Scholar
[G3-4] Gong, G., On inductive limit of matrix algebras over higher dimension spaces, Part I, II, Math Scand. 80(1997) 45–60, 61-100Google Scholar
[G5] Gong, G., On the classification of simple inductive limit C* -algebras. I. The reduction theorem. Doc. Math. 7(2002), 255–461. Google Scholar
[GJL] Gong, G., C. Jiang, and L. Li, A classification of inductive limit C* -algebras with ideal property. arxiv:1 607.07581 Google Scholar
[GJLP1] Gong, G., C. Jiang, L. Li, and C. Pasnicu, AT structure of AH algebras with the ideal property and torsion free K-theory. J. Funct. Anal. 58(2010), no. 6, 2119–2143. http://dx.doi.org/10.101 6/j.jfa.2009.11.01 6 Google Scholar
[GJLP2] Gong, G., A Reduction theorem for AH algebras with ideal property. arxiv:1607.07575Google Scholar
[Ji-Jiang] Ji, K. and C. Jiang, A complete classification of AI algebra with the ideal property. Canad. J. Math. 63(2011), no. 2,381-412. http://dx.doi.org/10.4153/CJM-2011-005-9 Google Scholar
[Jiang] Jiang, C., A classification ofnon simple C* -algebras oftracial rank one: inductive limit of finite direct sums of simple TAIC*-algebras. J. Topol. Anal. 3(2011), no. 3, 385–404. http://dx.doi.org/10.1142/S1 793525311000593 Google Scholar
[Lil] Li, L., On the classification of simple C* -algebras: inductive limit of matrix algebras trees. Mem. Amer. Math. Soc. 127(1997), no. 605. http://dx.doi.org/10.1090/memo/0605 Google Scholar
[Li2] Li, L., Simple inductive limit C*-algebras: spectra and approximation by interval algebras. J. Reine Angew Math 507(1999), 57–79. http://dx.doi.org/10.1515/crll.1 999.019 Google Scholar
[Li3] Li, L., Classification of simple C* -algebras: inductive limit of matrix algebras over one-dimensional spaces. J. Funct. Anal. 192(2002), no. 1,1-51. http://dx.doi.org/10.1006/jfan.2002.3895 Google Scholar
[Li4] Li, L., Reduction to dimension two of local spectrum for simple AH algebras. J. Ramanujan Math. Soc. 21(2006), no. 4, 365–390. Google Scholar
[Pasnicul] Pasnicu, C., On inductive limit of certain C* -algebras of the form C(x) F. Trans. Amer. Math. Soc. 310(1988), no. 2, 703–714. http://dx.doi.org/10.2307/2000987 Google Scholar
[Pasnicu2] Pasnicu, C., hape equivalence, nonstable K-theory and AH algebras. Pacific J. Math 192(2000), no. 1, 159–182. http://dx.doi.org/10.2140/pjm.2000.192.159 Google Scholar