Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-29T01:20:53.385Z Has data issue: false hasContentIssue false
  • English
  • Français

Perturbations of Von Neumann Subalgebras With Finite Index

Published online by Cambridge University Press:  20 November 2018

Shoji Ino
Shoji Ino*
Affiliation:
Department of Mathematical Sciences, Kyushu University, Motooka, Fukuoka, 819-0395, Japan e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study uniform perturbations of von Neumann subalgebras of a von Neumann algebra. Let 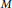$M$ and 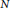$N$ be von Neumann subalgebras of a von Neumann algebra with finite probabilistic index in the sense of Pimsner and Popa. If 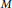$M$ and 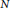$N$ are sufficiently close, then 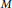$M$ and 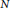$N$ are unitarily equivalent. The implementing unitary can be chosen as being close to the identity.

Keywords

46L1046L37von Neumann algebrasperturbations
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 59 , Issue 2 , 01 June 2016 , pp. 320 - 325
Copyright
Copyright © Canadian Mathematical Society 2016

References

[1] Choi, M. D. and Christensen, E., Completely order isomorphic and close C* -algebras need not be *-isomorphic.Bull. London Math. Soc. 15(1983), no. 6, 604–610. http://dx.doi.org/1 0.1112/blms/1 5.6.604 Google Scholar
[2] Cameron, J., Christensen, E., Sinclair, A. M., Smith, R. R., White, S., and Wiggins, A. D., Kadison-Kastler stable factors.Duke Math. J. 163(2014), 2639–2686. http://dx.doi.org/10.1215/00127094-2819736 Google Scholar
[3] Chan, W.-K., Perturbations of certain crossed product algebras by free groups. J. Funct. Anal. 267(2014), no. 10, 3994–4027.http://dx.doi.org/10.1016/j.jfa.2O14.09.014 Google Scholar
[4] Christensen, E., Perturbations of type I von Neumann algebras. J. London Math. Soc. 9(1974/75), 395–405.Google Scholar
[5] Christensen, E., Perturbation of operator algebras. Invent. Math. 43(1977), no. 1,1-13. http://dx.doi.org/10.1007/BF01390201 Google Scholar
[6] Christensen, E., Perturbation of operator algebras. II. Indiana Univ. Math. J. 26(1977), no. 5, 891–904. http://dx.doi.org/1 0.1 512/iumj.1 977.26.26072 Google Scholar
[7] Christensen, E., Near inclusions of C*-algebras. Acta Math. 144(1980), no. 3-4, 249–265. http://dx.doi.org/10.1007/BF02392125 Google Scholar
[8] Christensen, E., Sinclair, A. M., Smith, R. R., and White, S. A., Perturbations of C* -algebraic invariants. Geom. Funct. Anal. 20(2010), no. 2, 368–397. http://dx.doi.org/10.1OO7/sOOO39-O10-0070-y Google Scholar
[9] Christensen, E., Sinclair, A. M., Smith, R. R., White, S. A. and W Winter, Perturbations of nuclear C*-algebras. Acta Math. 208(2012), 93–150. http://dx.doi.org/10.1007/s11511-012-0075-5 Google Scholar
[10] Dickson, L., A Kadison Kastler row metric and intermediate subalgebras.Internat. J. Math. 25(2014), 140082, 16pp.http://dx.doi.org/10.1142/S0129167X14500827 Google Scholar
[11] Ino, S. and Watatani, Y., Perturbations of intermediate C*-subalgebras for simple C* -algebras. Bull. London Math. Soc. 46(2014), no. 3, 469–480. http://dx.doi.org/10.1112/blms/bduOO1 Google Scholar
[12] Johnson, B., Perturbations ofBanach algebras.Proc. London Math. Soc. 34(1977), no. 3, 439–458. http://dx.doi.org/10.1112/plms/s3-34.3.439 Google Scholar
[13] Johnson, B., A counterexample in the perturbation theory of C* -algebras. Canad.Math. Bull. 25(1982), 311–316. http://dx.doi.org/10.4153/CMB-1982-043-4 Google Scholar
[14] Jones, V. R. R., Index for subfactors. Invent. Math. 72(1983), no. 1,1-25. http://dx.doi.org/10.1007/BF01389127 Google Scholar
[15] Kadison, R. V. and Kastler, D., Perturbations of von Neumann algebras. I. Stability of type. Amer. J. Math. 94(1972), 38–54. http://dx.doi.org/10.2307/2373592 Google Scholar
[16] Khoshkam, M., On the unitary equivalence of close C* -algebras. Michigan Math. J. 31(1984), no. 3, 331–338. http://dx.doi.org/10.1307/mmj/1029003077 Google Scholar
[17] Kosaki, H., Extension of Jones theory on index to arbitrary factors.J. Funct. Anal. 66(1986), no. 1, 123–140. http://dx.doi.org/10.1016/0022-1236(86)90085-6 Google Scholar
[18] Phillips, J., Perturbations of type I von Neumann algebras. Pacific J. Math. 31(1979), 1012–1016. http://dx.doi.org/10.2140/pjm.1974.52.505 Google Scholar
[19] Phillips, J. and Raeburn, I., Perturbations of AF-algebras. Canad. J. Math. 31(1979), no. 5, 1012–1016. http://dx.doi.org/10.4153/CJM-1979-093-8 Google Scholar
[20] Phillips, J. and Raeburn, I., Perturbations of C*-algebras II. Proc. London Math. Soc. 43(1981), 46–72. http://dx.doi.org/10.1112/plms/s3-43.1.46 Google Scholar
[21] Pimsner, M. and Popa, S., Entropy and index for subfactors. Ann. Sci. Ecole Norm. Sup. 19(1986), 57–106.Google Scholar
[22] Popa, S., Classification of subfactors and their endomorphisms.CBMS Regional Conference Series in Mathematics, 86, American Mathematical Society, Providence, RI, 1995.Google Scholar
[23] Popa, S., The relative Dixmier property for inclusions of von Neumann algebras of finite index. Ann. Sci. École Norm. Sup. 32(1999), no. 6, 743–767. http://dx.doi.org/10.1016/S0012-9593(00)87717-4 Google Scholar
[24] Raeburn, I. and Taylor, J. L., Hochschildcohomology and perturbations ofBanach algebras. J. Funct.Anal. 25(1977), no. 3, 258–266. http://dx.doi.org/10.1016/0022-1236(77)90072-6 Google Scholar