Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-27T17:00:07.459Z Has data issue: false hasContentIssue false
  • English
  • Français

On Product of Radón Measures

Published online by Cambridge University Press:  20 November 2018

M. C. Godfrey  and
M. Sion
M. C. Godfrey
Affiliation:
University of British Columbia, Vancouver
M. Sion
Affiliation:
University of British Columbia, Vancouver
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let X, Y be locally compact Hausdorff spaces and μ, ν be Radón outer measures on X and Y respectively. The classical product outer measure ϕ on X × Y generated by measurable rectangles, without direct reference to the topology, turns out to have some serious drawbacks. For example, one can only prove that closed 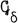sets (and hence Baire sets) are ϕ-measurable. It is unknown, even when X and Y are compact, whether closed sets are ϕ-measurable.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 4 , August 1969 , pp. 427 - 444
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Bledsoe, W. W. and Morse, A. P., Product measures. Trans. Amer. Math. Soc. 79 (1955) 173–215.Google Scholar
2. Bourbaki, N., Elements de mathématique: Livre VI, Intégration, Chap. I-IV. (Actual. Scient. Ind., No. 1175, Hermann, Paris, 1952.)Google Scholar
3. Edwards, R. E., A theory of Radón measures on locally compact spaces. Acta Math. 89 (1953) 133–164.Google Scholar
4. Halmos, P.R., Measure theory. (Van Nostrand, New York, 1950.)Google Scholar
5. Hewitt, E., Integration on locally compact spaces I, University of Washington Publications in Mathematics 3 (1952) 71–75.Google Scholar
6. Munroe, E. M., Introduction to measure and integration. (Addison-Wesley, Reading, 1953.)Google Scholar
7. Sierpinski, W., Sur le problème concernant les ensembles measurables superficiellement. Fund. Math. 1 (1920) 112–115.Google Scholar
8. Stromberg, K., A note on the convolution of regular measures. Math. Scand. 7 (1959) 347–352.Google Scholar