Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-30T01:50:45.488Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on the Diophantine Equation x2 + y6 = ze, e ≥ 4

Published online by Cambridge University Press:  20 November 2018

Konstantine Zelator
Konstantine Zelator*
Affiliation:
Department of Mathematics and Computer Science, Rhode Island College, Providence, RI 02908, USAe-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the diophantine equation 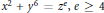${{x}^{2}}\,+\,{{y}^{6}}\,=\,{{z}^{e}},\,e\,\le \,4$. We show that, when $e$ is a multiple of 4 or 6, this equation has no solutions in positive integers with 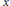$x$ and $y$ relatively prime. As a corollary, we show that there exists no primitive Pythagorean triangle one of whose leglengths is a perfect cube, while the hypotenuse length is an integer square.

Keywords

11Ddiophantine equation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 2 , 01 June 2012 , pp. 435 - 440
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Instructional conference and workshop on diophantine equations. Lorentz Center, Leiden University, The Netherlands. May 7–11, 2007 and May 14–16, 2007.Google Scholar
[2] Sierpinski, W., Elementary theory of numbers. North-Holland Mathematical Library, 31. North-Holland Publishing Co., Amsterdam; PWN—Polish Scientific Publishers, Warsaw, 1988, pp. 73–74, 78–79.Google Scholar
[3] Pocklington, H. C., Some diophantine impossibilities. Proc. Cambridge Philos. Soc. 17(1914), 108–121.Google Scholar
[4] Dickson, L. E., History of the theory of numbers. III. Quadratic and higher forms. AMS Chelsea Publishing, Providence, RI, 1992,Google Scholar