Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-27T13:52:42.428Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular Equations and Discrete, Genus-Zero Subgroups of SL(2, ℝ) Containing Γ(N)

Published online by Cambridge University Press:  20 November 2018

C. J. Cummins
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 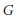$G$ be a discrete subgroup of 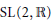$\text{SL}\left( 2,\,\mathbb{R} \right)$ which contains 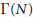$\Gamma \left( N \right)$ for some 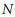$N$. If the genus of 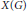$X\left( G \right)$ is zero, then there is a unique normalised generator of the field of 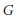$G$-automorphic functions which is known as a normalised Hauptmodul. This paper gives a characterisation of normalised Hauptmoduls as formal $q$ series using modular polynomials.

Keywords

11F0311F2230F35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 1 , 01 March 2002 , pp. 36 - 45
Copyright
Copyright © Canadian Mathematical Society 2002

Footnotes

The author was supported by NSERC and FCAR grants.

References

[B] Borcherds, R. E., Monstrous Moonshine and monstrous Lie superalgebras. Invent.Math. 109 (1992), 405–444.Google Scholar
[BR] Borcherds, R. E. and Ryba, A. J. E., Modular Moonshine II. DukeMath. J. 83 (1996), 435–459.Google Scholar
[CY] Chen, I. and Yui, N., Singular values of Thompson series. In: Groups, Difference sets and the Monster, (eds. K. T. Arusu et al), de Gruyter, 1995.Google Scholar
[C] Cohn, H., The primary role of modular equations. Number Theory, New York, 1991–1995, (eds. D. V. Chudnovsky, G. V. Chudnovsky, M. B. Nathanson), 19–41, Springer, New York, 1996.Google Scholar
[CM] Cohn, H. and McKay, J., Spontaneous generation of modular invariants. Math. Comp. 65 (1996), 1295–1309.Google Scholar
[CN] Conway, J. H. and Norton, S. P., Monstrous Moonshine. Bull. London Math. Soc. 11 (1979), 308–339.Google Scholar
[CG] Cummins, C. J. and Gannon, T.,Modular equations and the genus zero property of moonshine functions. Invent.Math. 129 (1997), 413–443.Google Scholar
[K] Kozlov, D. N., On completely replicable functions and extremal poset theory. M.Sc. thesis, Department of Math., University of Lund, Sweden, 1994.Google Scholar
[L] Lang, S., Elliptic functions. 2nd edition, Addison-Wesley, Reading, Massachusetts, 1987.Google Scholar
[Mah] Mahler, K., On a class of non-linear functional equations connected with modular functions. J. Austral.Math. Soc. Ser. A 22 (1976), 65–118.Google Scholar
[Mar] Martin, Y., On modular invariance of completely replicable functions. In: Moonshine, the Monster, and related Topics, (eds. C. Dong and G. Mason), Contemporary Mathematics 193, Amer. Math. Soc., Providence, RI, 1996, 263–286.Google Scholar
[N] Norton, S. P., Generalised Moonshine. Proc. Symp. Pure Math. 47, Part 1, The Arcata Conference on Representations of Finite Groups, Arcata, Calif., 1986, 210, Amer.Math. Soc., Providence, RI, 1987.Google Scholar
[Sh] Shimura, G., Introduction to the arithmetic theory of automorphic functions. Princeton University Press, 1971.Google Scholar
[T] Thompson, J. G., A finiteness theorem for subgroups of PSL(2, R) which are commensurable with PSL(2, Z). Proc. Sym. Pure.Math., 37, Santa Cruz Conference on finite groups, Amer. Math. Soc., Providence RI, 1980, 533–555.Google Scholar