Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-27T13:52:35.656Z Has data issue: false hasContentIssue false
  • English
  • Français

Irreducible Representations of Inner Quasidiagonal C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Bruce Blackadar  and
Eberhard Kirchberg
Bruce Blackadar
Affiliation:
Department of Mathematics, University of Nevada, Reno, Reno, NV, U.S.A. e-mail: [email protected]
Eberhard Kirchberg
Affiliation:
Institut für Mathematik, Humboldt Universität zu Berlin, Berlin, Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is shown that a separable 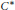${{C}^{*}}$-algebra is inner quasidiagonal if and only if it has a separating family of quasidiagonal irreducible representations. As a consequence, a separable 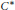${{C}^{*}}$-algebra is a strong 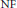$\text{NF}$ algebra if and only if it is nuclear and has a separating family of quasidiagonal irreducible representations. We also obtain some permanence properties of the class of inner quasidiagonal 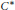${{C}^{*}}$-algebras.

Keywords

46L05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 3 , 01 September 2011 , pp. 385 - 395
Copyright
Copyright © Canadian Mathematical Society 2011

References

[Arv77] Arveson, W., Notes on extensions of C*-algebras. Duke Math. J. 44(1977), no. 2, 329–355. doi:10.1215/S0012-7094-77-04414-3Google Scholar
[BK97] Blackadar, B. and Kirchberg, E., Generalized inductive limits of finite-dimensional C*-algebras. Math. Ann. 307(1997), no. 3, 343–380. doi:10.1007/s002080050039Google Scholar
[BK01] Blackadar, B. and Kirchberg, E., Inner quasidiagonality and strong NF algebras. Pacific J. Math. 198(2001), no. 2, 307–329. doi:10.2140/pjm.2001.198.307Google Scholar
[Bla06] Blackadar, B., Operator algebras. Theory of C*-algebras and von Neumann algebras. In: Encyclopaedia of Mathematical Sciences, 122, Operator Algebras and Non-commutative Geometry, III, Springer-Verlag, Berlin, 2006.Google Scholar
[Dix69] Dixmier, J., Les C*-algèbres et leurs représentations. Cahiers Scientifiques, 29, Gauthier-Villars & Cie., Paris, 1964.Google Scholar
[Voi91] Voiculescu, D., A note on quasi-diagonal C*-algebras and homotopy. Duke Math. J. 62(1991), no. 2, 267–271. doi:10.1215/S0012-7094-91-06211-3Google Scholar
[Wea03] Weaver, N., A prime C*-algebra that is not primitive. J. Funct. Anal. 203(2003), no. 2, 356–361. doi:10.1016/S0022-1236(03)00196-4Google Scholar