Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-04-27T02:00:34.117Z Has data issue: false hasContentIssue false
  • English
  • Français

Differences between Perfect Powers

Published online by Cambridge University Press:  20 November 2018

Michael A. Bennett
Michael A. Bennett*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC, V6T 1Z2. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We apply the hypergeometric method of Thue and Siegel to prove that if $a$ and $b$ are positive integers, then the inequality 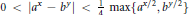$0\,<\,\left| {{a}^{x}}\,-\,{{b}^{y}} \right|\,<\,\frac{1}{4}\,\max \{{{a}^{x/2}},\,{{b}^{y/2}}\}$ has at most a single solution in positive integers $x$ and $y$. This essentially sharpens a classic result of LeVeque.

Keywords

11D6111D45
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 51 , Issue 3 , 01 September 2008 , pp. 337 - 347
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Bennett, M., Fractional parts of powers of rational numbers. Math. Proc. Cambridge Philos. Soc. 114(1993), no. 2, 191–201.Google Scholar
[2] Bennett, M., On some exponential equations of S. S. Pillai. Canad. J. Math. 53(2001), no. 5, 897–922.Google Scholar
[3] Beukers, F., Fractional parts of powers of rationals. Math. Proc. Cambridge Philos. Soc. 90(1981), no. 1, 13–20.Google Scholar
[4] Cassels, J. W. S., On the equation ax – by = 1 . Amer. J. Math. 75(1953), 159–162.Google Scholar
[5] Cassels, J. W. S., On the equation ax – by = 1. II. Proc. Cambridge Philos. Soc. 56(1960), 97–103.Google Scholar
[6] Ellison, W. J., On a theorem of S. Sivasankaranarayana Pillai. In: Séminaire de théorie des nombres, 1970-71. no. 12, Lab. Théorie des Nombres, Centre Nat. Recherche Sci., Talence, 1971.Google Scholar
[7] Herschfeld, A., The equation 2 x – 3 y = d. Bull. Amer. Math. Soc. 42(1936), no. 4, 231–234.Google Scholar
[8] Khinchin, A. Y., Continued Fractions. Third edition. P. Noordhoff Ltd., Groningen, 1963.Google Scholar
[9] Laurent, M., Mignotte, M., and Nesterenko, Y., Formes linéaires en deux logarithmes et déterminants d’interpolation. J. Number Theory 55(1995), no. 2, 285–321.Google Scholar
[10] LeVeque, W. J., On the equation ax – by = 1 . Amer. J. Math. 74(1952), 325–331.Google Scholar
[11] Mihăilescu, P., Primary cyclotomic units and a proof of Catalan's conjecture. J. Reine Angew.Math. 572(2004), 167–195.Google Scholar
[12] Pillai, S. S., On the inequality 0 < ax – by ≤ n. J. Indian Math. Soc. 19(1931), 1–11.Google Scholar
[13] Pillai, S. S., On ax – by = c. J. Indian Math. Soc. (N.S.) 2(1936), 119–122, 215.Google Scholar
[14] Pillai, S. S., On ax – bY = by ± ax J. Indian Math. Soc. (N.S.) 8(1944), 10–13.Google Scholar
[15] Pillai, S. S., On the equation 2 x – 3 y = 2 X + 3 Y . Bull. Calcutta Math. Soc. 37(1945), 18–20.Google Scholar
[16] Ribenboim, P., Catalan's Conjecture. Academic Press, Boston, MA, 1994.Google Scholar
[17] Scott, R. and Styer, R., On the generalized Pillai equation ±ax ± by = c J. Number Theory 118(2006), no. 2, 236–265.Google Scholar