Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-28T09:51:31.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Complexifying Lie Group Actions on Homogeneous Manifolds of Non-compact Dimension Two

Published online by Cambridge University Press:  20 November 2018

S. Ruhallah Ahmadi  and
Bruce Gilligan
S. Ruhallah Ahmadi
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK S4S 0A2 e-mail: [email protected]@gmail.com
Bruce Gilligan
Affiliation:
Department of Mathematics and Statistics, University of Regina, Regina, SK S4S 0A2 e-mail: [email protected]@gmail.com
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

If 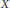$X$ is a connected complex manifold with 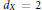${{d}_{X}}\,=\,2$ that admits a (connected) Lie group 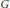$G$ acting transitively as a group of holomorphic transformations, then the action extends to an action of the complexification 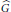$\widehat{G}$ of 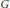$G$ on 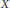$X$ except when either the unit disk in the complex plane or a strictly pseudoconcave homogeneous complex manifold is the base or fiber of some homogeneous fibration of 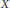$X$.

Keywords

32M10homogeneous complex manifoldnon-compact dimension twocomplexification
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 57 , Issue 4 , 01 December 2014 , pp. 673 - 682
Copyright
Copyright © Canadian Mathematical Society 2014

References

[Abe76] Abels, H., Proper transformation groups. In: Transformation groups. (Proc. Conf., Univ. Newcastle upon Tyne, Newcastle upon Tyne, 1976), London Math. Soc. Lecture Note Series, 26, Cambridge University Press, Cambridge, 1977, pp. 237–248.Google Scholar
[Abe82] Abels, H.,Some topological aspects of proper group actions; noncompact dimension of groups. J. London Math. Soc. (2) 25 (1982), no. 3, 525–538. http://dx.doi.org/10.1112/jlms/s2-25.3.525 Google Scholar
[Akh77] Ahiezer, D. N., Dense orbits with two endpoints. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 41 (1977), no. 2, 308–324, 477; Math. USSR-Izv. 11 (1977), no. 2, 293–307.Google Scholar
[Akh79] Ahiezer, D. N., Algebraic groups that are transitive in the complement to a homogeneous hypersurface. (Russian) Dokl. Akad. Nauk SSSR 245 (1979), no. 2, 281–284; Soviet Math. Dokl. 20 (1979), no. 2, 278–281.Google Scholar
[Akh83] Ahiezer, D. N., Complex n-dimensional homogeneous spaces homotopically equivalent to (2n-2)-dimensional compact manifolds. Selecta Math. Soviet 3(1983/84), no. 3, 286–290.Google Scholar
[Akh13] Ahiezer, D. N., Real group orbits on flag manifolds. In: Lie groups: structure, actions, and representations Progress in Mathematics, 306, Birkhäuser Basel, 2013, pp. 1–24.Google Scholar
[AG94] Akhiezer, D. and Gilligan, B., On complex homogeneous spaces with top homology in codimension two.Canad. J. Math. 46 (1994), no. 5, 897–919. http://dx.doi.org/10.4153/CJM-1994-051-x Google Scholar
[BoMo47] Bochner, S. and Montgomery, D., Groups on analytic manifolds. Ann. of Math. 48 (1947), 659–669. http://dx.doi.org/10.2307/1969133 Google Scholar
[Bor53] Borel, A., Les bouts des espaces homogánes de groupes de Lie. Ann. of Math. (2) 58 (1953), 443–457. http://dx.doi.org/10.2307/1969747 Google Scholar
[Che51] Chevalley, C., Théorie des groupes de Lie. Tome II. Groupes algébriques. Actualités Sci. Ind., 1152, Hermann &Cie., Paris, 1951.Google Scholar
[FHW] Fels, G., Huckleberry, A. T., and J. A.Wolf, Cycle spaces of flag domains. A complex geometric viewpoint. Progress in Mathematics, 245, Birkhäuser Boston, Inc., Boston, MA, 2006.Google Scholar
[Gil91] Gilligan, B., On the ends of complex manifolds homogeneous under a Lie group. In: Several complex variables and complex geometry, Part 2 (Santa Cruz, CA, 1989), Proc. Sympos. Pure Math., 52, American Mathematical Society, Providence, RI, 1991, pp. 217–224.Google Scholar
[Gil95] Gilligan, B., Complex homogeneous spaces of real groups with top homology in codimension two.Ann. Global Anal. Geom. 13 (1995), no. 3, 303–314. http://dx.doi.org/10.1007/BF00773662 Google Scholar
[GH98] Gilligan, B. and Heinzner, P., Globalization of holomorphic actions on principal bundles.Math. Nachr. 189 (1998), 145–156. http://dx.doi.org/10.1002/mana.19981890109 Google Scholar
[GH09] Gilligan, B. and Huckleberry, A. T., Fibrations and globalizations of compact homogeneous CR-Manifolds.(Russian) Izv. Ross. Akad. Nauk Ser. Mat. 73 (2009), no. 3, 67–126; translation in: Izv. Math. 73 (2009), no. 3, 501–553. http://dx.doi.org/10.4213/im2734 Google Scholar
[Hir70] Hironaka, H., Desingularizations of complex-analytic varieties. (French) In: Actes du Congrás International des Mathématiciens (Nice, 1970), Tome 2, Gauthier-Villars, Paris, 1971, pp. 627–631.Google Scholar
[Hoch65] Hochschild, G., The structure of Lie groups. Holden-Day Inc., San Franscisco-London-Amsterdam, 1965.Google Scholar
[HO81] Huckleberry, A. T. and Oeljeklaus, E., Homogeneous spaces from a complex analytic viewpoint. In: Manifolds and Lie groups. (Notre Dame, Ind., 1980) Progress in Math., 14, Birkhäuser, Boston, MA, 1981, pp. 159–186.Google Scholar
[HO84] Huckleberry, A. T. and Oeljeklaus, E., Classification theorems for almost homogeneous spaces. Institut E´ lie Cartan, 9, Universite´ de Nancy, Institut E´ lie Cartan, Nancy, 1984.Google Scholar
[HS81] Huckleberry, A. T. and Oeljeklaus, E. Huckleberry, A. T. and Snow, D., A classification of strictly pseudoconcave homogeneous manifolds.Ann. Scuola Norm. Sup. Pisa 8 (1981), no. 2, 231–255.Google Scholar
[HS82] Huckleberry, A. T. and Oeljeklaus, E. Huckleberry, A. T. and Snow, D., Almost-homogeneous Kähler manifolds with hypersurface orbits.Osaka J. Math. 19 (1982), no. 4, 763–786.Google Scholar
[Ka67] Kaup, W., Reelle Transformationsgruppen und invariante Metriken auf komplexen Räumen.Invent. Math. 3 (1967), 43–70. http://dx.doi.org/10.1007/BF01425490 Google Scholar
[Mal75] Malyshev, F. M., Complex homogeneous spaces of semisimple Lie groups of the first category. (Russian) Izv. Akad. Nauk SSSR, Ser. Mat. 39 (1975),no. 5, 992–1002, 1219; translation in: Math. USSR Izv. 9 (1977), no. 5, 939–949.Google Scholar
[Mal77] Malyshev, F. M., Complex homogeneous spaces of semisimple Lie groups of type Dn. (Russian) Izv. Akad. Nauk SSSR, Ser. Mat. 41 (1977), no. 4, 829–852, 959; translation in: Math. USSR Izv. 11 (1977), no. 4, 783–805.Google Scholar
[Mat79] Matsuki, T., The orbits of affine symmetric spaces under the action of minimal parabolic subgroups. J. Math. Soc. Japan 31 (1979), no. 2, 331–357. http://dx.doi.org/10.2969/jmsj/03120331 Google Scholar
[Mat82] Matsuki, T., Orbits on affine symmetric spaces under the action of parabolic subgroups. Hiroshima Math. J. 12 (1982), no. 2, 307–320.Google Scholar
[Mat60] Matsushima, Y., Espaces homogánes de Stein des groupes de Lie complexes.Nagoya Math. J. 16 (1960), 205–218.Google Scholar
[MN63] Morimoto, A. and Nagano, T.,On pseudo-conformal transformations of hypersurfaces.J. Math. Soc. Japan. 15 (1963), 289–300. http://dx.doi.org/10.2969/jmsj/01530289 Google Scholar
[Mos55] Mostow, G. D., On covariant fiberings of Klein spaces. Amer. J. Math. 77 (1955), 247–278. http://dx.doi.org/10.2307/2372530 Google Scholar
[Mos62] Mostow, G. D., Covariant fiberings of Klein spaces. II. Amer. J. Math. 84 (1962), 466–474. http://dx.doi.org/10.2307/2372983 Google Scholar
[OR84] Oeljeklaus, K. andRichthofer, W., Homogeneous complex surfaces. Math. Ann. 268 (1984), no. 3, 273–292. http://dx.doi.org/10.1007/BF01457059 Google Scholar
[Oni60] Onishchik, A. L., Complex hulls of compact homogeneous spaces. (Russian) Dokl. Akad. Nauk SSSR 130 (1960), 726–729; translation in: Soviet Math. Dokl. 1 (1960) 88–91.Google Scholar
[Oni62] Onishchik, A. L., Inclusion relations among transitive compact transformation groups. (Russian) Trudy Mosk. Mat. Obsc. 11 (1962), 199–242; translation in: Amer. Math. Soc. Transl. 50 (1966), 5–58.Google Scholar
[Oni69] Onishchik, A. L., Decompositions of reductive Lie groups. (Russian) Mat. Sb. 80 (122) (1969), 553–599; translation in: Math. USSR Sb. 9 (1969), 515–554.Google Scholar
[Ste82] Steinsiek, M., Transformation groups on homogeneous-rational manifolds. Math. Ann. 260 (1982), no. 4, 423–435. http://dx.doi.org/10.1007/BF01457022 Google Scholar
[Wan52] Wang, H.-C, Two-point homogeneous spaces.Ann. of Math. (2) 55 (1952), 177–191. http://dx.doi.org/10.2307/1969427 Google Scholar
[Weis66] Weisfeiler, B., On one class of unipotent subgroups of semisimple algebraic groups. arxiv:math/0005149v1; translated from Russian: Uspehi Mat. Nauk 21 (1966), 222–223.Google Scholar
[Wol69] Wolf, J. A., The action of a real semisimple group on a complex flag manifold. I. Orbit structure and holomorphic arc components. Bull. Amer. Math. Soc. 75 (1969), 1121–1237. http://dx.doi.org/10.1090/S0002-9904-1969-12359-1 Google Scholar