Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-28T08:24:40.575Z Has data issue: false hasContentIssue false
  • English
  • Français

Compact composition operators on model spaces

Part of: Holomorphic functions of several complex variables Special classes of linear operators Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  18 March 2025

Evgueni Doubtsov Open the ORCID record for Evgueni Doubtsov [Opens in a new window]
Evgueni Doubtsov*
Affiliation:
St. Petersburg Department of Steklov Mathematical Institute of Russian Academy of Sciences, Fontanka 27, St. Petersburg, 191023, Russia
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 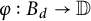$\varphi : B_d\to \mathbb {D}$, 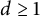$d\ge 1$, be a holomorphic function, where 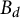$B_d$ denotes the open unit ball of 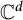$\mathbb {C}^d$ and 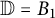$\mathbb {D}= B_1$. Let 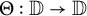$\Theta : \mathbb {D} \to \mathbb {D}$ be an inner function, and let 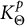$K^p_\Theta $ denote the corresponding model space. For 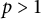$p>1$, we characterize the compact composition operators 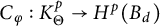$C_\varphi : K^p_\Theta \to H^p(B_d)$, where 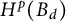$H^p(B_d)$ denotes the Hardy space.

Keywords

Model spacescomposition operatorNevanlinna counting functionreal interpolation of Banach spaces

MSC classification

Primary: 47B33: Composition operators 32A35: $H^p$-spaces, Nevanlinna spaces 46B70: Interpolation between normed linear spaces
Type
Article
Information
Canadian Mathematical Bulletin , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research was supported by the Russian Science Foundation (Grant No. 23-11-00171), https://rscf.ru/project/23-11-00171/.

References

Aleksandrov, A. B. and Doubtsov, E., Clark measures on the complex sphere . J. Funct. Anal. 278(2020), no. 2, 108314, 30.Google Scholar
Baranov, A. D., Embeddings of model subspaces of the Hardy class: compactness and Schatten–von Neumann ideals . Izv. Ross. Akad. Nauk Ser. Mat. 73(2009), no. 6, 3–28 (Russian); English transl.: Izv. Math. 73(2009), no. 6, 1077–1100.Google Scholar
Bergh, J. and Löfström, J., Interpolation spaces. An introduction . In B. Eckmann and J. K. Moser (eds.), Grundlehren der Mathematischen Wissenschaften, vol. 223, Springer-Verlag, Berlin and New York, 1976, x+207 pp.Google Scholar
Choe, B. R., The essential norms of composition operators . Glasgow Math. J. 34(1992), no. 2, 143–155.Google Scholar
Cohn, W. S., Carleson measures and operators on star-invariant subspaces . J. Operator Theory 15(1986), 181–202.Google Scholar
Cwikel, M., Real and complex interpolation and extrapolation of compact operators . Duke Math. J. 65(1992), no. 2, 333–343.Google Scholar
Kislyakov, S. V. and Zlotnikov, I. K., Interpolation for intersections of Hardy-type spaces . Israel J. Math. 239(2020), no. 1, 21–38.Google Scholar
Littlewood, J. E., On Inequalities in the Theory of Functions . Proc. London Math. Soc. (2) 23(1925), no. 7, 481–519.Google Scholar
Lyubarskii, Y. I. and Malinnikova, E., Composition operators on model spaces. Recent trends in analysis. In: A. Borichev, K. R. Davidson, S. Kupin, G. Pisier, F.-H. Vasilescu, V. Vasyunin (eds.), Theta Ser. Adv. Math., vol. 16, Theta, Bucharest, 2013, pp. 149–157.Google Scholar
Shapiro, J. H., The essential norm of a composition operator . Ann. of Math. (2) 125(1987), no. 2, 375–404.Google Scholar