Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-29T13:44:23.097Z Has data issue: false hasContentIssue false
  • English
  • Français

Values of Twisted Tensor L-functions of Automorphic Forms Over Imaginary Quadratic Fields

Published online by Cambridge University Press:  20 November 2018

Dominic Lanphier ,
Howard Skogman  and
Hiroyuki Ochiai
Dominic Lanphier
Affiliation:
Department of Mathematics, Western Kentucky UniversityBowling Green, KY 42101. e-mail: [email protected]
Howard Skogman
Affiliation:
Department of Mathematics, SUNY Brockport, BrockportNY 14420. e-mail: [email protected]
Hiroyuki Ochiai
Affiliation:
Institute of Mathematics for Industry, Kyushu University, Motooka, Fukuoka, 819-0395, Japan. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 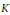$K$ be a complex quadratic extension of 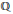$\mathbb{Q}$ and let 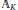${{\mathbb{A}}_{K}}$ denote the adeles of 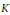$K$. We find special values at all of the critical points of twisted tensor $L$-functions attached to cohomological cuspforms on 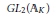$G{{L}_{2}}\left( {{\mathbb{A}}_{K}} \right)$ and establish Galois equivariance of the values. To investigate the values, we determine the archimedean factors of a class of integral representations of these $L$-functions, thus proving a conjecture due to Ghate. We also investigate analytic properties of these $L$-functions, such as their functional equations.

Keywords

11F6711F37twisted tensor L-functioncuspform, hypergeometric series
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 5 , 01 October 2014 , pp. 1078 - 1109
Copyright
Copyright © Canadian Mathematical Society 2014

References

[1] Andrews, G. E., Askey, R., and Roy, R., Special functions. Encyclopedia of Mathematics and its Applications, 71, Cambridge Univeristy Press, Cambridge, 1999.Google Scholar
[2] Asai, T., On certain Dirichlet series associated with Hilbert modular forms and Rankin's method. Math. Ann. 226(1977), no. 1, 81–94.http://dx.doi.org/10.1007/BF01391220 Google Scholar
[3] Deligne, P., Valeurs de fonctions Let priodes d'intègrales. In: Automorphic forms, automorphic representations, and L-Functions (Proc. Symp. Pure Math. Oregon State Univ., Corvallis, Ore, 1977), part 2, American Mathematical Society, Providence, RI, 1979, pp. 313–346.Google Scholar
[4] Flicker, Y. Z., On zeroes of the twisted tensor L-function. Math. Ann. 297(1993), no. 2, 199–219.http://dx.doi.org/10.1007/BF01459497 Google Scholar
[5] Flicker, Y .Z. and Zinoviev, D., On poles of twisted tensor L-functions. Proc. Japan Acad. Ser. A Math. Sci. 71(1995), no. 6, 114–116.http://dx.doi.org/10.3792/pjaa.71.114 Google Scholar
[6] Ghate, E., Critical Values of the Asai L-function in the imaginary quadratic case. Thesis (Ph.D.), University of California, Los Angeles, Proquest LLC, Ann Arbor, MI, 1996.Google Scholar
[7] Ghate, E., Critical values of the twisted tensor L-function in the imaginary quadratic case. Duke Math J. 96(1999), no. 3, 595–638.http://dx.doi.org/10.1215/S0012-7094-99-09619-9 Google Scholar
[8] Ghate, E., Critical values of twisted tensor L-functions over CM-fields. In: Automorphic forms, automorphic representations, and arithmetic (FortWorth, TX, 1996), Proc. Symp. Pure Math., 66, Part 1, American Mathematical Society, Providence, RI, 1999, pp. 87–109.Google Scholar
[9] Harder, G., Eisenstein cohomology of arithmetic groups. The case GL2. Invent. Math. 89(1987), no. 1, 37–118. http://dx.doi.org/10.1007/BF01404673 Google Scholar
[10] Hida, H., p-Ordinary cohomology groups for SL(2) over number fields. Duke Math. J. 69(1993), no. 2,259–314. http://dx.doi.org/10.1215/S0012-7094-93-06914-1 Google Scholar
[11] Hida, H., On the critical values of L-functions of GL(2) and GL(2)✗ GL(2). Duke Math. J. 74(1994), no. 2, 431–528. http://dx.doi.org/10.1215/S0012-7094-94-07417-6 Google Scholar
[12] Knuth, D. E., The art of computer programming. Addison-Wesley, Reading, Mass, 1968.Google Scholar
[13] Krishnamurthy, M., The Asai transfer to GL4 via the Langlands-Shahidi method. Int. Math. Res. Not. 2003, no. 41, 2221–2254.Google Scholar
[14] Mahnkopf, J., Cohomology of arithmetic groups, parabolic subgroups and special values of L-functions of GLn. J. Inst. Math. Jussieu 4(2005), no. 4, 553–637.http://dx.doi.org/10.1017/S1474748005000186 Google Scholar
[15] Miyake, T., Modular forms. Springer-Verlag, Berlin, 1989.Google Scholar
[16] Raghuram, A. and Shahidi, F., On certain period relations for cusp forms on GLn. Int. Math. Res. Not. IMRN 2008, Art. ID rnn 077, 23 pp.Google Scholar
[17] Shimura, G., The critical values of certain Dirichlet series attached to Hilbert modular forms. Duke Math. J. 63(1991), no. 3, 557–613. http://dx.doi.org/10.1215/S0012-7094-91-06324-6 Google Scholar
[18] Shimura, G., On modular forms of half-integral weight. Ann. Math. 97(1973), 440–481.http://dx.doi.org/10.2307/1970831 Google Scholar
[19] Takase, K., On certain Dirichlet series associated with automorphic forms on SL(2; C). Manuscripta Math. 56(1986), no. 3, 293–312. http://dx.doi.org/10.1007/BF01180770 Google Scholar
[20] Zhao, Y., Certain Dirichlet series attached to automorphic forms over imaginary quadratic fields. Duke Math. J. 72(1993), no. 3, 695–724.http://dx.doi.org/10.1215/S0012-7094-93-07226-2 Google Scholar