Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-05-03T07:06:02.809Z Has data issue: false hasContentIssue false
  • English
  • Français

Thompson’s semigroup and the first Hochschild cohomology

Part of: Abstract harmonic analysis Linear spaces and algebras of operators Special classes of linear operators

Published online by Cambridge University Press:  07 March 2024

Linzhe Huang
Linzhe Huang*
Affiliation:
Beijing Institute of Mathematical Sciences and Applications, Beijing 101408, China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we apply the theory of algebraic cohomology to study the amenability of Thompson’s group 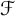$\mathcal {F}$. We introduce the notion of unique factorization semigroup which contains Thompson’s semigroup 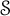$\mathcal {S}$ and the free semigroup 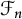$\mathcal {F}_n$ on n (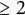$\geq 2$) generators. Let 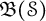$\mathfrak {B}(\mathcal {S})$ and 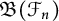$\mathfrak {B}(\mathcal {F}_n)$ be the Banach algebras generated by the left regular representations of 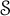$\mathcal {S}$ and 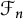$\mathcal {F}_n$, respectively. We prove that all derivations on 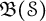$\mathfrak {B}(\mathcal {S})$ and 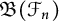$\mathfrak {B}(\mathcal {F}_n)$ are automatically continuous, and every derivation on 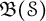$\mathfrak {B}(\mathcal {S})$ is induced by a bounded linear operator in 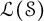$\mathcal {L}(\mathcal {S})$, the weak-operator closed Banach algebra consisting of all bounded left convolution operators on 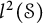$l^2(\mathcal {S})$. Moreover, we prove that the first continuous Hochschild cohomology group of 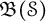$\mathfrak {B}(\mathcal {S})$ with coefficients in 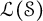$\mathcal {L}(\mathcal {S})$ vanishes. These conclusions provide positive indications for the left amenability of Thompson’s semigroup.

Keywords

AmenabilityderivationBanach algebraThompson’s semigroupcohomology group

MSC classification

Primary: 47L10: Algebras of operators on Banach spaces and other topological linear spaces 47B37: Operators on special spaces (weighted shifts, operators on sequence spaces, etc.) 43A07: Means on groups, semigroups, etc.; amenable groups
Type
Article
Information
Canadian Journal of Mathematics , Volume 77 , Issue 3 , June 2025 , pp. 842 - 862
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by Beijing Municipal Science & Technology Commission (Grant No. Z221100002722017) and by a grant from Beijing Institute of Mathematical Sciences and Applications. This research was also supported partly by the AMSS of Chinese Academy of Sciences and by YMSC of Tsinghua University.

References

Bade, W. G. and Curtis, P. C. Jr., The continuity of derivations of Banach algebras . J. Funct. Anal. 16(1974), 372–387.CrossRefGoogle Scholar
Brin, M. G. and Squier, C. C., Groups of piecewise linear homeomorphisms of the real line . Invent. Math. 79(1985), 485–498.CrossRefGoogle Scholar
Cannon, J. W., Floyd, W. J., and Parry, W. R., Introductory notes on Richard Thompson’s groups . Enseign. Math. (2) 42(1996), 215–256.Google Scholar
Christensen, E., Pop, F., Sinclair, A. M., and Smith, R. R., Hochschild cohomology of factors with property $\varGamma$ . Ann. of Math. (2) 158(2003), 635–659.CrossRefGoogle Scholar
Dong, A., Huang, L., and Xue, B., Operator algebras associated with multiplicative convolutions of arithmetic functions . Sci. China Math. 61(2018), 1665–1676.CrossRefGoogle Scholar
Følner, E., On groups with full Banach mean value . Math. Scand. 3(1955), 243–254.CrossRefGoogle Scholar
Frey, A. H., Studies on amenable semigroups. Ph.D. thesis, University of Washington, 1960.Google Scholar
Ge, L., Numbers and figures (in Chinese). In: Xi, N., The institute lecture 2010, Science Press, Beijing, 2012, pp. 1–10.Google Scholar
Ge, L., Ma, M., and Qi, B., Riemann $\zeta$ -functions on semigroups (in Chinese) . Sci. Sin. Math. 51(2021), 1545–1578.Google Scholar
Hochschild, G., On the cohomology groups of an associative algebra , Ann. of Math. (2) 46(1945), 58–67.CrossRefGoogle Scholar
Hochschild, G., On the cohomology theory for associative algebras , Ann. of Math. (2) 47(1946), 568–579.CrossRefGoogle Scholar
Hochschild, G., Cohomology and representations of associative algebras . Duke Math. J. 14(1947), 921–948.CrossRefGoogle Scholar
Johnson, B. E., Cohomology in Banach algebras, Memoirs of the American Mathematical Society, American Mathematical Society, Providence, RI, 1972.CrossRefGoogle Scholar
Johnson, B. E., A class of ${\rm II}_1$ factors without property $P$ but with zero second cohomology . Ark. Mat. 12(1974), 153–159.CrossRefGoogle Scholar
Johnson, B. E., Kadison, R. V., and Ringrose, J. R., Cohomology of operator algebras III. Reduction to normal cohomology . Bull. Soc. Math. France 100(1972), 73–96.CrossRefGoogle Scholar
Johnson, B. E. and Sinclair, A. M., Continuity of derivations and a problem of Kaplansky . Amer. J. Math. 90(1968), 1067–1973.CrossRefGoogle Scholar
Kadison, R. V., On the orthogonalization of operator representations . Amer. J. Math. 77(1955), 600–620.CrossRefGoogle Scholar
Kadison, R. V., Derivations of operator algebras . Ann. of Math. 83(1966), 280–293.CrossRefGoogle Scholar
Kadison, R. V. and Ringrose, J. R., Cohomology of operator algebras I: Type I von Neumann algebras . Acta Math. 126(1971), 227–243.CrossRefGoogle Scholar
Kadison, R. V. and Ringrose, J. R., Cohomology of operator algebras II: Extended cobounding and the hyperfinite case . Ark. Mat. 9(1971), 55–63.CrossRefGoogle Scholar
Kaplansky, I., Modules over operator algebras . Amer. J. Math. 75(1953), 839–859.CrossRefGoogle Scholar
Pop, F. and Smith, R. R., Vanishing of second cohomology for tensor products of type II ${}_1$ von Neumann algebras . J. Funct. Anal. 258(2010), 2695–2707.CrossRefGoogle Scholar
Sakai, S., On a conjecture of Kaplansky . Tohoku Math. J. (2) 12(1960), 31–33.CrossRefGoogle Scholar
Sakai, S., Derivations of W ${}^{\ast }$ -Algebras . Ann. of Math. (2) 83(1966), 273–279.CrossRefGoogle Scholar
Sinclair, A. M. and Smith, R. R., Hochschild cohomology of von Neumann algebras, Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Sinclair, A. M. and Smith, R. R., Hochschild cohomology for von Neumann algebras with Cartan subalgebras . Amer. J. Math. 120(1998), 1043–1057.CrossRefGoogle Scholar
Xue, B., Non-commutative arithmetics on Thompson’s monoid . Acta Math. Sin. (Engl. Ser.) 37(2021), 1586–1626.CrossRefGoogle Scholar