Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-04-29T08:58:56.486Z Has data issue: false hasContentIssue false
  • English
  • Français

Sub-Bergman Hilbert spaces on the unit disk III

Part of: Special classes of linear operators Spaces and algebras of analytic functions

Published online by Cambridge University Press:  22 August 2023

Shuaibing Luo  and
Kehe Zhu Open the ORCID record for Kehe Zhu [Opens in a new window]
Shuaibing Luo*
Affiliation:
School of Mathematics, Hunan University, Changsha, Hunan 410082, China
Kehe Zhu
Affiliation:
Department of Mathematics and Statistics, State University of New York, Albany, NY 12222, USA e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For a bounded analytic function 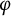$\varphi $ on the unit disk 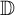$\mathbb {D}$ with 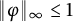$\|\varphi \|_\infty \le 1$, we consider the defect operators 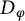$D_\varphi $ and 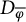$D_{\overline \varphi }$ of the Toeplitz operators 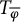$T_{\overline \varphi }$ and 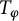$T_\varphi $, respectively, on the weighted Bergman space 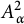$A^2_\alpha $. The ranges of 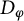$D_\varphi $ and 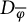$D_{\overline \varphi }$, written as 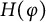$H(\varphi )$ and 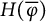$H(\overline \varphi )$ and equipped with appropriate inner products, are called sub-Bergman spaces.

We prove the following three results in the paper: for 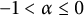$-1<\alpha \le 0$, the space 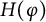$H(\varphi )$ has a complete Nevanlinna–Pick kernel if and only if 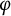$\varphi $ is a Möbius map; for 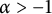$\alpha>-1$, we have 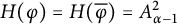$H(\varphi )=H(\overline \varphi )=A^2_{\alpha -1}$ if and only if the defect operators 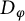$D_\varphi $ and 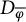$D_{\overline \varphi }$ are compact; and for 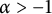$\alpha>-1$, we have 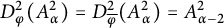$D^2_\varphi (A^2_\alpha )= D^2_{\overline \varphi }(A^2_\alpha )=A^2_{\alpha -2}$ if and only if 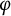$\varphi $ is a finite Blaschke product. In some sense, our restrictions on 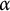$\alpha $ here are best possible.

Keywords

Bergman spaceNevanlinna–Pick kernelToeplitz operatordefect operatorsub-Bergman spaces

MSC classification

Primary: 30H15: Nevanlinna class and Smirnov class 30H10: Hardy spaces 30H05: Bounded analytic functions 47B35: Toeplitz operators, Hankel operators, Wiener-Hopf operators
Secondary: 30H25: Besov spaces and $Q_p$-spaces 30H30: Bloch spaces 47B07: Operators defined by compactness properties
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 5 , October 2024 , pp. 1520 - 1537
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

S. Luo was supported by the National Natural Science Foundation of China (Grant No. 12271149). K. Zhu was supported by the National Natural Science Foundation of China (Grant No. 12271328).

References

Abkar, A. and Jafarzadeh, B., Weighted sub-Bergman Hilbert spaces in the unit disk . Czechoslov. Math. J. 60(2010), 435–443.CrossRefGoogle Scholar
Agler, J. and McCarthy, J. E., Complete Nevanlinna–Pick kernels . J. Funct. Anal. 175(2000), 111–124.CrossRefGoogle Scholar
Agler, J. and McCarthy, J. E., Pick interpolation and Hilbert function spaces, Graduate Studies in Mathematics, 44, American Mathematical Society, Providence, RI, 2002.CrossRefGoogle Scholar
Aleman, A., Hartz, M., McCarthy, J. E., and Richter, S., The Smirnov class for spaces with the complete Pick property . J. Lond. Math. Soc. (2) 96(2017), 228–242.CrossRefGoogle Scholar
Aleman, A., Hartz, M., McCarthy, J. E., and Richter, S., Factorizations induced by complete Nevanlinna–Pick factors . Adv. Math. 335(2018), 372–404.CrossRefGoogle Scholar
Aleman, A., Hartz, M., McCarthy, J. E., and Richter, S., Interpolating sequences in spaces with the complete Pick property . Int. Math. Res. Not. IMRN 12(2019), 3832–3854.CrossRefGoogle Scholar
Aleman, A., Hartz, M., McCarthy, J. E., and Richter, S., Weak products of complete Pick spaces . Indiana Univ. Math. J. 70(2021), 325–352.CrossRefGoogle Scholar
Chu, C., Density of polynomials in sub-Bergman Hilbert spaces . J. Math. Anal. Appl. 467(2018), 699–703.CrossRefGoogle Scholar
Chu, C., Hilbert spaces contractively contained in weighted Bergman spaces on the unit disk . J. Math. Anal. Appl. 472(2019), 386–394.CrossRefGoogle Scholar
Chu, C., Which de Branges–Rovnyak spaces have complete Nevanlinna–Pick property? J. Funct. Anal. 279(2020), no. 6, Article no. 108608, 15 pp.CrossRefGoogle Scholar
de Branges, L., A proof of the Bieberback conjecture . Acta Math. 154(1985), 137–152.CrossRefGoogle Scholar
Fricain, E. and Mashreghi, J., The theory of $\mathbf{\mathcal{H}}(b)$ spaces. Vols. 1 and 2, New Mathematical Monographs, 20 and 21, Cambridge University Press, Cambridge, 2016.Google Scholar
Gu, C., Vector-valued sub-Bergman spaces on the unit disk. Preprint.Google Scholar
Gu, C., Hwang, I. S., Lee, W. Y., and Park, J., Higher-order de Branges–Rovnyak and sub-Bergman spaces . Adv. Math. 428(2023), Article no. 109143.CrossRefGoogle Scholar
Hartz, M., On the isomorphism problem for multiplier algebras of Nevanlinna–Pick spaces . Can. J. Math. 69(2017), no. 1, 54–106.CrossRefGoogle Scholar
Hartz, M., Private communication, 2023.Google Scholar
Luo, S., Gu, C., and Richter, S., Higher order local Dirichlet integrals and de Branges–Rovnyak spaces . Adv. Math. 385(2021), Article no. 107748, 47 pp.CrossRefGoogle Scholar
Nowak, M. and Rososzczuk, R., Weighted sub-Bergman Hilbert spaces . Ann. Univ. Mariae Curie-Skłodowska Sect. A 68(2014), no. 1, 49–57.Google Scholar
Paulsen, V. I. and Raghupathi, M., An introduction to the theory of reproducing kernel Hilbert spaces, Cambridge Studies in Advanced Mathematics, 152, Cambridge University Press, Cambridge, 2016.CrossRefGoogle Scholar
Rososzczuk, R. and Symesak, F., Weighted sub-Bergman Hilbert spaces in the unit ball of ${\mathbb{C}}^n$ . Concr. Oper. 7(2020), no. 1, 124–132.CrossRefGoogle Scholar
Sarason, D., Sub-hardy Hilbert spaces in the unit disk, Wiley, New York, 1994.Google Scholar
Sultanic, S., Sub-Bergman Hilbert spaces . J. Math. Anal. Appl. 324(2006), 639–649.CrossRefGoogle Scholar
Symesak, F., Sub-Bergman spaces in the unit ball of ${\mathbb{C}}^n$ . Proc. Amer. Math. Soc. 138(2010), no. 12, 4405–4411.CrossRefGoogle Scholar
Zhao, R. and Zhu, K., Theory of Bergman spaces in the unit ball of ${\mathbb{C}}^n$ . Mem. Soc. Math. France 115(2008), 103.CrossRefGoogle Scholar
Zhu, K., Sub-Bergman Hilbert spaces on the unit disk . Indiana Univ. Math. J. 45(1996), 165–176.CrossRefGoogle Scholar
Zhu, K., Sub-Bergman Hilbert spaces in the unit disk II . J. Funct. Anal. 202(2003), 327–341.CrossRefGoogle Scholar
Zhu, K., Operator theory in function spaces, Mathematical Surveys and Monographs, 138, American Mathematical Society, Providence, RI, 2007.CrossRefGoogle Scholar