Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-29T19:51:42.438Z Has data issue: false hasContentIssue false
  • English
  • Français

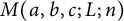Some inequalities between $M(a,b,c;L;n)$ and the partition function $p(n)$

Part of: Additive number theory; partitions

Published online by Cambridge University Press:  10 December 2024

Bing He Open the ORCID record for Bing He [Opens in a new window] ,
Linpei Li  and
Jian Cao Open the ORCID record for Jian Cao [Opens in a new window]
Bing He*
Affiliation:
School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha 410083, Hunan, People’s Republic of China e-mail: [email protected]
Linpei Li
Affiliation:
School of Mathematics and Statistics, HNP-LAMA, Central South University, Changsha 410083, Hunan, People’s Republic of China e-mail: [email protected]
Jian Cao
Affiliation:
School of Mathematics, Hangzhou Normal University, Hangzhou 311121, People’s Republic of China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let $p(n)$ and $M(m,L;n)$ be the number of partitions of n and the number of partitions of n with crank congruent to m modulo L, respectively, and let

$$ \begin{align*}M(a,b,c;L;n):= M(a,L;n) + M(b,L;n) + M(c,L;n).\end{align*} $$

In this paper, we focus on some relations between $M(m,L;n)$ and $p(n),$ which Dyson, Andrews, and Garvan etc. have studied previously. By applying a modification of the circle method to estimate the Fourier coefficients of generating functions, we establish the following inequalities between 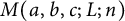$M(a,b,c;L;n)$ and 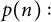$p(n):$ for $n \geq 467$,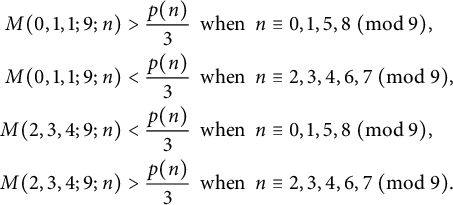

$$ \begin{align*} M(0,1,1;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(0,1,1;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n) < \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 0,1,5,8 ~ (\mathrm{mod}~9), \\ M(2,3,4;9;n)> \frac{p(n)}{3} &\;\: \mathrm{when}\;\: n \equiv 2,3,4,6,7 ~ (\mathrm{mod}~9). \end{align*} $$

In the proof of these inequalities, an inequality for the logarithm of the generating function for $p(n)$ is derived and applied. Our method reduces the last possible counterexamples to $467 \leq n \leq 22471$, and it will produce more effective estimates when proving inequalities of such types.

Keywords

InequalitypartitioncrankM(a, b, c;L;n)p(n)circle method

MSC classification

Primary: 11P55: Applications of the Hardy-Littlewood method 11P82: Analytic theory of partitions
Secondary: 11P83: Partitions; congruences and congruential restrictions
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 23
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Andrews, G. A. and Lewis, R., The ranks and cranks of partitions moduli 2, 3, and 4 . J. Number Theory 85(2000), no. 1, 74–84.CrossRefGoogle Scholar
Andrews, G. E. and Berndt, B. C., Ramanujan’s lost notebook. Part III, Springer, New York, 2012.CrossRefGoogle Scholar
Andrews, G. E. and Garvan, F. G., Dyson’s crank of a partition . Bull. Amer. Math. Soc. (N.S.) 18(1988), no. 2, 167–171.CrossRefGoogle Scholar
Apostol, T. M., Modular functions and Dirichlet series in number theory, Graduate Texts in Mathematics, Vol. 41, second edition, Springer-Verlag, New York, 1990.CrossRefGoogle Scholar
Atkin, A. O. L. and Swinnerton-Dyer, P., Some properties of partitions . Proc. London Math. Soc. (3) 4(1954), 84–106.CrossRefGoogle Scholar
Aygin, Z. S. and Chan, S. H., Combinations of ranks and cranks of partitions moduli 6, 9 and 12 and their comparison with the partition function . Ann. Comb. 23(2019), nos. 3–4, 489–509.CrossRefGoogle Scholar
Borozenets, N., Deviation of the rank and crank modulo 11. Preprint, 2023, arXiv:2305.08751v3.CrossRefGoogle Scholar
Bringmann, K. and Pandey, B.V., Biases among classes of rank-crank partitions (mod11) . J. Math. Anal. Appl. 536(2024), no. 2, Paper No. 128221, 17 pp.CrossRefGoogle Scholar
Chan, O.-Y., Some asymptotics for cranks . Acta Arith. 120(2005), no. 2, 107–143.CrossRefGoogle Scholar
Chan, S. H. and Mao, R., Inequalities for ranks of partitions and the first moment of ranks and cranks of partitions . Adv. Math. 258(2014), 414–437.CrossRefGoogle Scholar
Chen, N., Chern, S., Fan, Y. and Xia, E. X. W., Some generating functions and inequalities for the Andrews-Stanley partition functions . Proc. Edinb. Math. Soc. (2) 65(2022), no. 1, 120–135.CrossRefGoogle Scholar
Dyson, F. J., Some guesses in the theory of partitions . Eureka 8(1944), 10–15.Google Scholar
Fan, Y., Xia, E. X. W. and Zhao, X., New equalities and inequalities for the ranks and cranks of partitions . Adv. in Appl. Math. 146(2023), Paper No. 102486, 37 pp.CrossRefGoogle Scholar
Kane, D. M., Resolution of a conjecture of Andrews and Lewis involving cranks of partitions . Proc. Amer. Math. Soc. 132(8)( 2004), 2247–2256.CrossRefGoogle Scholar
Kang, S.-Y., Mock Jacobi forms in basic hypergeometric series . Compos. Math. 145(2009), no. 3, 553–565.CrossRefGoogle Scholar
Mao, R., Ranks of partitions modulo 10 . J. Number Theory 133(2013), no. 11, 3678–3702.CrossRefGoogle Scholar
Rademacher, H., On the expansion of the partition function in a series . Ann. of Math. (2) 44(1943), 416–422.CrossRefGoogle Scholar
Schlosser, M. J. and Zhou, N.H., On the infinite Borwein product raised to a positive real power . Ramanujan J. 61(2023), no. 2, 515–543.CrossRefGoogle ScholarPubMed
Yao, O. X. M., Personal communications, 2023.Google Scholar
Zhou, N. H., On the distribution of rank and crank statistics for integer partitions . Res. Number Theory 5(2019), no. 2, Paper No. 18, 8 pp.CrossRefGoogle Scholar
Zhou, N. H., On the distribution of the rank statistic for strongly concave compositions . Bull. Aust. Math. Soc. 100(2019), no. 2, 230–238.CrossRefGoogle Scholar