Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-30T15:56:34.449Z Has data issue: false hasContentIssue false
  • English
  • Français

Singular Integral Operators and Essential Commutativity on the Sphere

Published online by Cambridge University Press:  20 November 2018

Jingbo Xia
Jingbo Xia*
Affiliation:
Department of Mathematics, State University of New York at Buffalo, Buffalo, NY 14260, USA, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 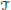$\mathcal{T}$ be the 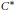${{C}^{*}}$-algebra generated by the Toeplitz operators 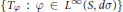$\left\{ {{T}_{\varphi }}:\varphi \in {{L}^{\infty }}\left( S,d\sigma \right) \right\}$ on the Hardy space 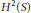${{H}^{2}}\left( S \right)$ of the unit sphere in 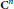${{C}^{n}}$. It is well known that 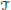$\mathcal{T}$ is contained in the essential commutant of 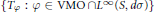$\left\{ {{T}_{\varphi }}:\varphi \in \text{VMO}\cap {{L}^{\infty }}\left( S,d\sigma \right) \right\}$. We show that the essential commutant of 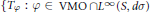$\left\{ {{T}_{\varphi }}:\varphi \in \text{VMO}\cap {{L}^{\infty }}\left( S,d\sigma \right) \right\}$ is strictly larger than 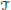$\mathcal{T}$.

Keywords

32A5546L0547L80
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 62 , Issue 4 , 01 August 2010 , pp. 889 - 913
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Calderón, A.-P., Inequalities for the maximal function relative to a metric. Studia Math. 57(1976), no. 3, 297–306.Google Scholar
[2] Coifman, R. and Fefferman, C., Weighted norm inequalities for maximal functions and singular integrals. Studia Math. 51(1974), 241–250.Google Scholar
[3] Coifman, R., Rochberg, R., and Weiss, G., Factorization theorems for Hardy spaces in several variables. Ann. of Math. 103(1976), no. 3, 611–635. doi:10.2307/1970954Google Scholar
[4] Coifman, R. and Weiss, G., Analyse harmonique non-commutative sur certains espaces homogènes. Lecture Notes in Mathematics 242. Springer-Verlag, Berlin, 1971.Google Scholar
[5] Conway, J., Functions of One Complex Variable. Second edition. Graduate Texts in Mathematics 11. Springer-Verlag, New York, 1978.Google Scholar
[6] Davidson, K., On operators commuting with Toeplitz operators modulo the compact operators. J. Functional. Analysis 24(1977), no. 3, 291–02. doi:10.1016/0022-1236(77)90060-XGoogle Scholar
[7] Ding, X. and Sun, S., Essential commutant of analytic Toeplitz operators. Chinese Sci. Bull. 42(1997), no. 7, 548–552.Google Scholar
[8] Engliš, M., Toeplitz operators and the Berezin transform on H2. Linear Algebra Appl. 223/224(1995), 171–204. doi:10.1016/0024-3795(94)00056-JGoogle Scholar
[9] Garnett, J., Bounded Analytic Functions. Pure and Applied Mathematics 96. Academic Press, New York, 1981.Google Scholar
[10] Guo, K. and Sun, S., The essential commutant of the analytic Toeplitz algebra and some problems related to it. (Chinese) Acta Math. Sinica (Chin. Ser.) 39(1996), no. 3, 300–313.Google Scholar
[11] Johnson, B. and Parrott, S., Operators commuting with a von Neumann algebra modulo the set of compact operators. J. Functional Analysis 11(1972), 39–61. doi:10.1016/0022-1236(72)90078-XGoogle Scholar
[12] Korányi, A. and Vági, S., Singular integrals on homogeneous spaces and some problems of classical analysis. Ann. Scuola Norm. Sup. Pisa 25(1971), 575–648.Google Scholar
[13] Muckenhoupt, B., Weighted norm inequalities for the Hardy maximal function. Trans. Amer. Math. Soc. 165(1972), 207–226. doi:10.2307/1995882Google Scholar
[14] Muhly, P. and Xia, J., On automorphisms of the Toeplitz algebra. Amer. J. Math. 122(2000), no. 6, 1121–1138. doi:10.1353/ajm.2000.0047Google Scholar
[15] Popa, S., The commutant modulo the set of compact operators of a von Neumann algebra. J. Funct. Anal. 71(1987), no. 2, 393–408. doi:10.1016/0022-1236(87)90011-5Google Scholar
[16] Rudin, W., Function Theory in the Unit Ball of C n. Grundlehren der Mathematischen Wissenschaften 241. Springer-Verlag, New York, 1980.Google Scholar
[17] Stein, E., Harmonic Analysis: Real-Variable Methods, Orthogonality, and Oscillatory Integrals. Princeton Mathematical Series 43. Princeton University Press, Princeton, 1993.Google Scholar
[18] Voiculescu, D., A non-commutative Weyl-von Neumann theorem. Rev. Roumaine Math. Pures Appl. 21(1976), no. 1, 97–113.Google Scholar
[19] Xia, J., Coincidence of essential commutant and the double commutant relation in the Calkin algebra. J. Funct. Anal. 197(2003), no. 1, 140–150. doi:10.1016/S0022-1236(02)00034-4Google Scholar
[20] Xia, J., Bounded functions of vanishing mean oscillation on compact metric spaces. J. Funct. Anal. 209(2004), no. 2, 444–467. doi:10.1016/j.jfa.2003.08.006Google Scholar
[21] Xia, J., On the essential commutant of T(QC). Trans. Amer. Math. Soc. 360(2008), no. 2, 1089–1102. doi:10.1090/S0002-9947-07-04345-0Google Scholar