Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-05-02T22:20:45.823Z Has data issue: false hasContentIssue false
  • English
  • Français

On Limit Multiplicities for Spaces of Automorphic Forms

Published online by Cambridge University Press:  20 November 2018

Anton Deitmar  and
Werner Hoffmann
Anton Deitmar
Affiliation:
Math. Inst. d. Universität, Im Neuenheimer Feld 288, 69126 Heidelberg, Germany email: [email protected]
Werner Hoffmann
Affiliation:
Humboldt-Universität zu Berlin, Institut für Mathematik, Jägerstr. 10/11, 10117 Berlin, Germany email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $\Gamma $ be a rank-one arithmetic subgroup of a semisimple Lie group $G$. For fixed 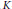$K$-Type, the spectral side of the Selberg trace formula defines a distribution on the space of infinitesimal characters of $G$, whose discrete part encodes the dimensions of the spaces of square-integrable $\Gamma $-automorphic forms. It is shown that this distribution converges to the Plancherel measure of $G$ when $\Gamma $ shrinks to the trivial group in a certain restricted way. The analogous assertion for cocompact lattices $\Gamma $ follows from results of DeGeorge-Wallach and Delorme.

Keywords

11F7222E3022E4043A8558G25limit multiplicitiesautomorphic formsnoncompact quotientsSelberg trace formulafunctional calculus
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 51 , Issue 5 , 01 October 1999 , pp. 952 - 976
Copyright
Copyright © Canadian Mathematical Society 1999

References

[1] Arthur, J., The Selberg trace formula for groups of F-rank one. Ann. of Math. 100(1974), 326–385.Google Scholar
[2] Arthur, J., A trace formula for reductive groups I: Terms associated to classes in G(Q). DukeMath. J. 45(1978), 911–952.Google Scholar
[3] Arthur, J., A trace formula for reductive groups II: Applications of a truncation operator. Comp. Math. 40(1980), 87–121.Google Scholar
[4] Arthur, J., The trace formula in invariant form. Ann. of Math. 114(1981), 1–74.Google Scholar
[5] Arthur, J., On a family of distributions obtained from Eisenstein series II. Amer. J. Math. 104(1982), 1289–1336.Google Scholar
[6] Arthur, J., A Paley-Wiener theorem for real reductive groups. Acta Math. 150(1983), 1–89.Google Scholar
[7] Arthur, J., A measure on the unipotent variety. Canad. J. Math. 37(1985), 1237–1274.Google Scholar
[8] Arthur, J., The local behaviour of weighted orbital integrals. Duke Math. J. 56(1988), 223–293.Google Scholar
[9] Clozel, L. and Delorme, P., Le théorème de Paley-Wiener invariant pour les groupes de Lie reductifs. Invent. Math. 77(1984), 427–453.Google Scholar
[10] DeGeorge, D. and Wallach, N., Limit formulas for multiplicities in L2(Γ \ G). Ann. Math. 107(1978), 133–150.Google Scholar
[11] DeGeorge, D. and Wallach, N., Limit formulas for multiplicities in L2(Γ \ G) II. Ann.Math. 109(1979), 477–495.Google Scholar
[12] Deitmar, A. and Hoffmann, W., Spectral estimates for towers of noncompact quotients. Canad. J. Math. (2) 51(1999), 266–293.Google Scholar
[13] Delorme, P., Formules limites et formules asymptotiques pour les multiplicites dans L2(Γ \ G). Duke Math. J. 53(1986), 691–731.Google Scholar
[14] Dixmier, J., Les C*algèbres et leur représentations.2ieme ed., Gauthier, Paris, 1969.Google Scholar
[15] Hejhal, D., The Selberg trace formula for PSL2(R), vol. II. Lecture Notes in Math. 1001, Springer, 1983.Google Scholar
[16] Hejhal, D., A continuity method for spectral theory on Fuchsian groups. Modular Forms (ed. Rankin, R.), Horwood, Chichester, 1984, 107–140.Google Scholar
[17] Helgason, S., Groups and Geometric Analysis. Academic Press, 1984.Google Scholar
[18] Hoffmann, W., An invariant trace formula for rank one lattices. Math. Nachr., to appear.Google Scholar
[19] Huxley, M., Scattering matrices for Congruence Subgroups. In: Modular Forms (ed. Rankin, R.), Horwood, Chichester, 1984, 141–156.Google Scholar
[20] Huxley, M., Exceptional eigenvalues and congruence subgroups. The Selberg trace formula and related topics, Contemp.Math. 53(1986), 341–349.Google Scholar
[21] Iwaniec, H., Non-holomorphic modular forms and their applications. In: Modular Forms (ed. Rankin, R.), Horwood, Chichester, 1984, 157–196.Google Scholar
[22] Iwaniec, H., Small eigenvalues of Laplacian for Γ0(N). Acta Arith. 56(1990), 65–82.Google Scholar
[23] Luo, W., Rudnick, Z. and Sarnak, P., On Selberg's eigenvalue conjecture. Geom. Funct. Anal. 5(1995), 387–401.Google Scholar
[24] Miatello, R., The Minakshisundaram-Pleijel coefficients for the vector-valued heat kernel on compact locallysymmetric spaces of negative curvature. Trans. Amer.Math. Soc. 260(1980), 1–33.Google Scholar
[25] Minemura, K., Invariant differential operators and spherical sections on a homogeneous vector bundle. Tokyo J. Math. 15(1992), 231–245.Google Scholar
[26] Müller, W., The trace class conjecture in the theory of automorphic forms. Ann.Math. 130(1989), 473–529.Google Scholar
[27] Müller, W., On the singularities of residual intertwining operators. Preprint.Google Scholar
[28] Phillips, R. and Sarnak, P., On cusp forms for co-finite subgroups of PSL(2, R). Invent.Math. 80(1985), 339–364.Google Scholar
[29] Phillips, R. and Sarnak, P., Perturbation theory for the Laplacian on automorphic functions. J. Amer.Math. Soc. 5(1992), 1–32.Google Scholar
[30] Prachar, K., Primzahlverteilung. Grundlehren Math.Wiss. 91, Springer, 1957.Google Scholar
[31] Sarnak, P., A Note on the Spectrum of Cusp Forms for Congruence Subgroups. Preprint, 1983.Google Scholar
[32] Sarnak, P., On cusp forms. The Selberg trace formula and related topics, Contemp.Math. 53(1986), 393–407.Google Scholar
[33] Savin, G., Limit multiplicities of cusp forms. Invent.Math. 95(1989), 149–162.Google Scholar
[34] Selberg, A., Harmonic analysis. Collected papers 1, Springer, 1989, 626–674.Google Scholar
[35] Taylor, M., Partial Differential Equations I. Springer, 1996.Google Scholar
[36] Wallach, N., Limit multiplicities in L2(Γ\G). Cohomology of arithmetic groups and automorphic forms (Proc. Conf. Luminy/Fr., 1989), Lecture Notes in Math. 1447(1990), 31–56.Google Scholar
[37] Yang, A., Poisson transforms on vector bundles. Trans. Amer.Math. Soc. 350(1998), 857–887.Google Scholar