Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-01T19:54:34.721Z Has data issue: false hasContentIssue false
  • English
  • Français

On Gap Properties and Instabilities of p-Yang–Mills Fields

Published online by Cambridge University Press:  20 November 2018

Qun Chen  and
Zhen-Rong Zhou
Qun Chen
Affiliation:
School of Mathematics and Statistics, Wuhan University, Wuhan 430072, P. R. China email: [email protected]
Zhen-Rong Zhou
Affiliation:
School of Mathematics and Statistics, Central China Normal University, Wuhan 430079, P. R. China email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the 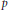$p$-Yang-Mills functional 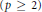$\left( p\,\ge \,2 \right)$ defined as 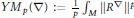$Y{{M}_{p}}(\nabla ):=\frac{1}{p}{{\int }_{M}}{{\left\| {{R}^{\nabla }} \right\|}^{p}}$. We call critical points of 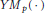$Y{{M}_{p}}(\cdot )$ the p-Yang–Mills connections, and the associated curvature 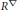${{R}^{\nabla }}$ the 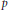$p$-Yang-Mills fields. In this paper, we prove gap properties and instability theorems for 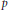$p$-Yang-Mills fields over submanifolds in 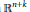${{\mathbb{R}}^{n+k}}$ and 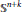${{\mathbb{S}}^{n+k}}$.

Keywords

58E1553C05p-Yang–Mills fieldgap propertyinstabilitysubmanifold
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 6 , 01 December 2007 , pp. 1245 - 1259
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Bourguignon, J.-P., Lawson, H. B., and Simons, J., Stability and gap phenomena for Yang-Mills fields. Proc. Nat. Acad. Sci. U.S.A. 76(1979), no. 4, 1550–1553.Google Scholar
[2] Bourguignon, J.-P. and Lawson, H. B., Stability and isolation phenomena for Yang-Mills fields. Comm. Math. Phys. 79(1981), no. 2, 189–230.Google Scholar
[3] Kobayashi, S., Ohnita, Y., and Takeuchi, M., On instability of Yang-Mills connections. Math. Z. 193(1986), no. 2, 165–189.Google Scholar
[4] Shen, C. L., Weak stability of Yang-Mills fields over submanifolds of the sphere. Arch. Math. 39(1982), no. 1, 78–84.Google Scholar
[5] Sacks, J. and Uhlenbeck, K., The existence of minimal immersions of 2-spheres. Ann. of Math. 113(1981), no.1, 1–24.Google Scholar
[6] Uhlenbeck, K., Connections with Lp bounds on curvature. Comm. Math. Phys. 83(1982), no. 1, 31–42.Google Scholar
[7] Wei, S. W., Representing homotopy groups and spaces of maps by p-harmonic maps. Indiana Univ. Math. J. 47(1998), no. 2, 625–670.Google Scholar
[8] Xin, Y. L., Instability theorems of Yang-Mills fields. Acta Math. Sci. 3(1983), no.1, 103–112.Google Scholar