Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-02T15:44:22.390Z Has data issue: false hasContentIssue false
  • English
  • Français

Heat kernel asymptotics for real powers of Laplacians

Part of: Partial differential equations on manifolds; differential operators

Published online by Cambridge University Press:  23 January 2023

Cipriana Anghel Open the ORCID record for Cipriana Anghel [Opens in a new window]
Cipriana Anghel*
Affiliation:
Institute of Mathematics of the Romanian Academy, Bucharest, Romania
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe the small-time heat kernel asymptotics of real powers 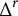$\operatorname {\Delta }^r$, 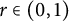$r \in (0,1)$ of a non-negative self-adjoint generalized Laplacian 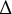$\operatorname {\Delta }$ acting on the sections of a Hermitian vector bundle 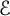$\mathcal {E}$ over a closed oriented manifold M. First, we treat separately the asymptotic on the diagonal of $M \times M$ and in a compact set away from it. Logarithmic terms appear only if n is odd and r is rational with even denominator. We prove the non-triviality of the coefficients appearing in the diagonal asymptotics, and also the non-locality of some of the coefficients. In the special case 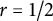$r=1/2$, we give a simultaneous formula by proving that the heat kernel of 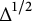$\operatorname {\Delta }^{1/2}$ is a polyhomogeneous conormal section in $\mathcal {E} \boxtimes \mathcal {E}^* $ on the standard blow-up space 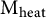$\operatorname {M_{heat}}$ of the diagonal at time 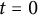$t=0$ inside 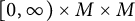$[0,\infty )\times M \times M$.

Keywords

Heat kernel asymptoticsfractional powers of Laplaciansblow-up heat spacepolyhomogeneous expansions

MSC classification

Primary: 58J37: Perturbations; asymptotics 58J35: Heat and other parabolic equation methods
Type
Article
Information
Canadian Journal of Mathematics , Volume 76 , Issue 2 , April 2024 , pp. 367 - 393
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was partially supported from the project PN-III-P4-ID-PCE-2020-0794 funded by UEFSCDI.

References

Agronovič, M. S., Some asymptotic formulas for elliptic pseudodifferential operators . Funktsional. Anal. i Prilozhen. 21(1987), 63–65.Google Scholar
Bär, C. and Moroianu, S., Heat kernel asymptotics for roots of generalized Laplacians . Int. J. Math. 14(2003), 397–412.CrossRefGoogle Scholar
Bellman, R., A brief introduction to theta functions, Athena Series: Selected Topics in Mathematics, Holt, Rinehart and Winston, New York, 1961.Google Scholar
Berger, M., Gauduchon, P., and Mazet, E., Le spectre d’une variété riemannienne, Lecture Notes in Mathematics, 194, Springer, Berlin and New York, 1971.CrossRefGoogle Scholar
Berline, N., Getzler, E., and Vergne, M., Heat kernels and Dirac operators, Springer, Berlin, 2004.Google Scholar
Berline, N. and Vergne, M., A computation of the equivariant index of the Dirac operator . Bull. Soc. Math. France 113(1985), 305–345.CrossRefGoogle Scholar
Bismut, J. M., The Atiyah–Singer theorems: a probabilistic approach . J. Funct. Anal. 57(1984), 329–348.CrossRefGoogle Scholar
Bourguignon, J., Hijazi, O., Milhorat, J., Moroianu, A., and Moroianu, S., A spinorial approach to Riemannian and conformal geometry, European Mathematical Society, Zurich, 2015.CrossRefGoogle Scholar
Chandrasekharan, K. and Narasimhan, R., Hecke’s functional equation and arithmetical identities . Ann. Math. 74(1961), 1–23.CrossRefGoogle Scholar
Duistermaat, J. J. and Guillemin, V. W., The spectrum of positive elliptic operators and periodic bicharacteristics . Invent. Math. 29(1975), 39–79.CrossRefGoogle Scholar
Fahrenwaldt, M. A., Off-diagonal heat kernel asymptotics of pseudodifferential operators on closed manifolds and subordinate Brownian motion . Integr. Equ. Oper. Theory 87(2017), 327–347.CrossRefGoogle Scholar
Getzler, E., Pseudodifferential operators on supermanifolds and the index theorem . Commun. Math. Phys. 92(1983), 163–178.CrossRefGoogle Scholar
Gilkey, P. B., Invariance theory, the heat equation, and the Atiyah–Singer index theorem. 2nd ed., Studies in Advanced Mathematics, CRC Press, Boca Raton, FL, 1995.Google Scholar
Gilkey, P. B. and Grubb, G., Logarithmic terms in asymptotic expansions of heat operator traces . Comm. Partial Differential Equations 23(1998), nos. 5–6, 777–792.CrossRefGoogle Scholar
Grieser, D., Basics of the b-calculus . In: Gil, J. B., Grieser, D., and Lesch, M. (eds.), Approaches to singular analysis, Advances in Partial Differential Equations, Birkhäuser, Basel, 2001, pp. 30–84.CrossRefGoogle Scholar
Grubb, G., Functional calculus of pseudo-differential boundary problems, Progress in Mathematics, 65, Birkhäuser, Boston, MA, 1986.CrossRefGoogle Scholar
Loya, P., Moroianu, S., and Ponge, R., On the singularities of the zeta and eta functions of an elliptic operator . Int. J. Math. 23(2012), no. 6, 1250020.CrossRefGoogle Scholar
Melrose, R. B., Calculus of conormal distributions on manifolds with corners . Int. Math. Res. Not. 3(1992), 51–61.CrossRefGoogle Scholar
Melrose, R. B., The Atiyah–Patodi–Singer index theorem, Research Notes in Mathematics, 4, A K Peters, Ltd., Wellesley, MA, 1993.CrossRefGoogle Scholar
Melrose, R. B. and Mazzeo, R. R., Analytic surgery and the eta invariant . Geom. Funct. Anal. 5(1995), no. $1$ , 14–75.Google Scholar
Minakshisundaram, S. and Pleijel, A., Some properties of the eigenfunctions of the Laplace operator on Riemannian manifolds . Can. J. Math. 1(1949), 242–256.CrossRefGoogle Scholar
Paris, R. B. and Kaminski, D., Asymptotics and Mellin–Barnes integrals, Cambridge University Press, Cambridge, 2001.CrossRefGoogle Scholar
Whittaker, E. T. and Watson, G. N., A course of modern analysis, Cambridge University Press, Cambridge, 1965.Google Scholar