Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-29T22:48:46.885Z Has data issue: false hasContentIssue false
  • English
  • Français

Fourier coefficients of minimal and next-to-minimal automorphic representations of simply-laced groups

Part of: Lie groups Discontinuous groups and automorphic forms Linear algebraic groups and related topics

Published online by Cambridge University Press:  21 September 2020

Dmitry Gourevitch ,
Henrik P. A. Gustafsson ,
Axel Kleinschmidt ,
Daniel Persson  and
Siddhartha Sahi
Dmitry Gourevitch
Affiliation:
Faculty of Mathematics and Computer Science, Weizmann Institute of Science, POB 26, Rehovot76100, Israel e-mail: [email protected] URL: http://www.wisdom.weizmann.ac.il/~dimagur
Henrik P. A. Gustafsson
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA94305-2125, USA [left September 2019] and School of Mathematics, Institute for Advanced Study, Princeton, NJ08540, USA and Department of Mathematics, Rutgers University, Piscataway, NJ08854, USA and Department of Mathematical Sciences, University of Gothenburg and Chalmers University of Technology, GothenburgSE-412 96, Sweden e-mail: [email protected] URL: http://hgustafsson.se
Axel Kleinschmidt
Affiliation:
Max-Planck-Institut für Gravitationsphysik (Albert-Einstein-Institut), Am Mühlenberg 1, DE-14476 Potsdam, GermanyInternational Solvay Institutes, ULB-Campus Plaine CP231, BE-1050, Brussels, Belgium e-mail: [email protected]
Daniel Persson*
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology, SE-412 96 Gothenburg, Sweden
Siddhartha Sahi
Affiliation:
Department of Mathematics, Rutgers University, Hill Center—Busch Campus, 110 Frelinghuysen Road Piscataway, NJ08854-8019, USA e-mail: [email protected]
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we analyze Fourier coefficients of automorphic forms on a finite cover G of an adelic split simply-laced group. Let 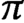$\pi $ be a minimal or next-to-minimal automorphic representation of G. We prove that any 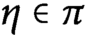$\eta \in \pi $ is completely determined by its Whittaker coefficients with respect to (possibly degenerate) characters of the unipotent radical of a fixed Borel subgroup, analogously to the Piatetski-Shapiro–Shalika formula for cusp forms on 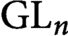$\operatorname {GL}_n$ . We also derive explicit formulas expressing the form, as well as all its maximal parabolic Fourier coefficient, in terms of these Whittaker coefficients. A consequence of our results is the nonexistence of cusp forms in the minimal and next-to-minimal automorphic spectrum. We provide detailed examples for G of type 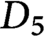$D_5$ and 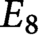$E_8$ with a view toward applications to scattering amplitudes in string theory.

Keywords

Automorphic functionsmall representationsminimal representationnext-to-minimal representationFourier coefficientWhittaker coefficientWhittaker supportnilpotent orbitwave-front setstring theory

MSC classification

Primary: 11F30: Fourier coefficients of automorphic forms
Secondary: 11F70: Representation-theoretic methods; automorphic representations over local and global fields 22E55: Representations of Lie and linear algebraic groups over global fields and adèle rings 20G45: Applications to physics
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 1 , February 2022 , pp. 122 - 169
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

References

Ahlén, O., Gustafsson, H. P. A., Kleinschmidt, A., Liu, B., and Persson, D., Fourier coefficients attached to small automorphic representations of ${SL}_n(A)$ . J. Number Theory 192(2018), 80–142.CrossRefGoogle Scholar
Brylinski, J.-L. and Deligne, P., Central extensions of reductive groups by K2. Publ. Math. Inst. Hautes Études Sci. 94(2001), 5–85.CrossRefGoogle Scholar
Bao, L., Kleinschmidt, A., Nilsson, B. E. W., Persson, D., and Pioline, B., Instanton corrections to the universal hypermultiplet and automorphic forms on SU(2,1). Commun. Number Theory Phys. 4(2010), 187–266.CrossRefGoogle Scholar
Bourbaki, N., Éléments de mathématique. Fasc. XXXVIII: Groupes et algèbres de Lie. Chapitre VII: Sous-algèbres de Cartan, éléments réguliers. Chapitre VIII: Algèbres de Lie semi-simples déployées. In: Actualités Scientifiques et Industrielles, Vol. 1364, Hermann, Paris, 1975.Google Scholar
Bossard, G. and Pioline, B., Exact ${\nabla}^4{R}^4$ couplings and helicity supertraces. J. High Energy Phys. 1(2017), 50.CrossRefGoogle Scholar
Collingwood, D. H. and McGovern, W. M., Nilpotent orbits in semisimple Lie algebras . Van Nostrand Reinhold Mathematics Series, Van Nostrand Reinhold Company, New York, NY, 1993.Google Scholar
D’Hoker, E., Green, M. B., and Vanhove, P., On the modular structure of the genus-one type II superstring low energy expansion. J. High Energy Phys. 8(2015), 41.CrossRefGoogle Scholar
Fleig, P., Gustafsson, H. P. A., Kleinschmidt, A., and Persson, D., Eisenstein series and automorphic representations . Cambridge Studies in Advanced Mathematics, 176, Cambridge University Press, Cambridge, UK, 2018.CrossRefGoogle Scholar
Fleig, P., Kleinschmidt, A., and Persson, D., Fourier expansions of Kac-Moody Eisenstein series and degenerate Whittaker vectors. Commun. Number Theory Phys. 8(2014), 41–100.CrossRefGoogle Scholar
Green, M. B. and Gutperle, M., Effects of D instantons. Nucl. Phys. B 498(1997), 195–227.CrossRefGoogle Scholar
Green, M. B. and Gutperle, M., D Particle bound states and the D instanton measure. J. High Energy Phys. 1(1998), 5.CrossRefGoogle Scholar
Gourevitch, D., Gustafsson, H. P. A., Kleinschmidt, A., Persson, D., and Sahi, S., A reduction principle for Fourier coefficients of automorphic forms. Preprint, 2018. arXiv:1811.05966v3 Google Scholar
Gourevitch, D., Gustafsson, H. P. A., Kleinschmidt, A., Persson, D., and Sahi, S., Eulerianity of Fourier coefficients of automorphic forms. Preprint, 2020. arXiv:2004.14244 CrossRefGoogle Scholar
Gomez, R., Gourevitch, D., and Sahi, S., Whittaker supports for representations of reductive groups. Annales de l'Institut Fourier, to appear. arXiv:1610.00284 Google Scholar
Gomez, R., Gourevitch, D., and Sahi, S., Generalized and degenerate Whittaker models. Compos. Math. 153(2017), no. 2, 223–256.CrossRefGoogle Scholar
Ginzburg, D., Certain conjectures relating unipotent orbits to automorphic representations. Israel J. Math. 151(2006), 323–355.CrossRefGoogle Scholar
Ginzburg, D., Towards a classification of global integral constructions and functorial liftings using the small representations method. Adv. Math. 254(2014), 157–186.CrossRefGoogle Scholar
Gustafsson, H. P. A., Kleinschmidt, A., and Persson, D., Small automorphic representations and degenerate Whittaker vectors. J. Number Theory 166(2016), 344–399.CrossRefGoogle Scholar
Green, M. B., Miller, S. D., and Vanhove, P., Small representations, string instantons, and Fourier modes of Eisenstein series. J. Number Theory 146(2015), 187–309.CrossRefGoogle Scholar
Ginzburg, D., Rallis, S., and Soudry, D., On the automorphic theta representation for simply laced groups. Israel J. Math. 100(1997), 61–116.CrossRefGoogle Scholar
Ginzburg, D., Rallis, S., and Soudry, D., The descent map from automorphic representations of GL(n) to classical groups . World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2011.CrossRefGoogle Scholar
Gan, W. T. and Savin, G., On minimal representations definitions and properties. Represent. Theory 9(2005), 46–93.CrossRefGoogle Scholar
Gourevitch, D. and Sahi, S., Generalized and degenerate Whittaker quotients and Fourier coefficients. In: Representations of reductive groups, Proc. Sympos. Pure Math, 101, Amer. Math. Soc., Providence, RI, 2019, pp. 133–154.CrossRefGoogle Scholar
Green, M. B. and Vanhove, P., Duality and higher derivative terms in M theory. J. High Energy Phys. 1(2006), no. 93, 37.Google Scholar
Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York, NY-Heidelberg, Germany, 1977.Google Scholar
Hull, C. M. and Townsend, P. K., Unity of superstring dualities. Nucl. Phys. B 438(1995), 109–137.CrossRefGoogle Scholar
Jiang, D., Liu, B., and Savin, G., Raising nilpotent orbits in wave-front sets. Represent. Theory 20(2016), 419–450.CrossRefGoogle Scholar
Kazhdan, D. and Polishchuk, A., Minimal representations: spherical vectors and automorphic functionals. In: Algebraic groups and arithmetic . Tata Inst. Fund. Res., Mumbai, 2004, pp. 127–198.Google Scholar
Kobayashi, T. and Savin, G., Global uniqueness of small representations. Math. Z. 281(2015), nos. 1–2, 215–239.CrossRefGoogle Scholar
Kostov, I. K. and Vanhove, P., Matrix string partition functions. Phys. Lett. B 444(1998), 196–203.CrossRefGoogle Scholar
Li, J.-S., Nonexistence of singular cusp forms. Compos. Math. 83(1992), no. 1, 43–51.Google Scholar
Matumoto, H., Whittaker vectors and associated varieties. Invent. Math. 89(1987), no. 1, 219–224.CrossRefGoogle Scholar
Moore, G. W., Nekrasov, N., and Shatashvili, S., D particle bound states and generalized instantons. Commun. Math. Phys. 209(2000), 77–95.CrossRefGoogle Scholar
Miller, S. D. and Sahi, S., Fourier coefficients of automorphic forms, character variety orbits, and small representations. J. Number Theory 132(2012), no. 12, 3070–3108.CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Modèles de Whittaker dégénérés pour des groupes $p$ -adiques. Math. Z. 196(1987), no. 3, 427–452.CrossRefGoogle Scholar
Mœglin, C. and Waldspurger, J.-L., Spectral decomposition and Eisenstein series . Cambridge Tracts in Mathematics, 113, Cambridge University Press, Cambridge, UK, 1995. Une paraphrase de l’Écriture [A paraphrase of Scripture].CrossRefGoogle Scholar
Ðoković, D. Ž., Note on rational points in nilpotent orbits of semisimple groups. Indag. Math. (N.S.) 9(1998), no. 1, 31–34.Google Scholar
Persson, D., Automorphic instanton partition functions on Calabi-Yau threefolds. J. Phys. Conf. Ser. 346(2012), 012016.CrossRefGoogle Scholar
Pioline, B., R4 couplings and automorphic unipotent representations. J. High Energy Phys. 3(2010), 116.CrossRefGoogle Scholar
Pioline, B. and Persson, D., The automorphic NS5-brane. Commun. Number Theory Phys. 3(2009), 697–754.Google Scholar
Piatetski-Shapiro, I. I., Multiplicity one theorems. In: Automorphic forms, representations and L-functions (Proc. Sympos. Pure Math., Oregon State Univ., Corvallis, Ore., 1977), Part 1, Proc. Sympos. Pure Math., Vol. XXXIII, Amer. Math. Soc., Providence, RI, 1979, pp. 209–212.Google Scholar
Rossmann, W., Picard-Lefschetz theory and characters of a semisimple Lie group. Invent. Math. 121(1995), no. 3, 579–611.CrossRefGoogle Scholar
Salmasian, H., A notion of rank for unitary representations of reductive groups based on Kirillov’s orbit method. Duke Math. J. 136(2007), no. 1, 1–49.CrossRefGoogle Scholar
Shalika, J. A., The multiplicity one theorem for GLn . Ann. Math. 100(1974), 171–193.CrossRefGoogle Scholar
Varma, S., On a result of Moeglin and Waldspurger in residual characteristic 2. Math. Z. 277(2014), nos. 3–4, 1027–1048.CrossRefGoogle Scholar
Weissman, M. H., L-groups and parameters for covering groups. Astérisque 398(2018), 33–186. L-groups and the Langlands program for covering groups.Google Scholar