Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-04-28T18:25:04.965Z Has data issue: false hasContentIssue false
  • English
  • Français

Differentiability of the operator norm on $\ell _p$ spaces

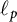Part of: Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  16 December 2024

Sreejith Siju
Sreejith Siju*
Affiliation:
Kerala School of Mathematics, Kozhikode, 673 571, India
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we present a characterization of strong subdifferentiability of the norm of bounded linear operators on 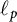$\ell _p$ spaces, 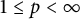$1\leq p<\infty $. Furthermore, we prove that the set of all bounded linear operators in 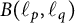${B}(\ell _p, \ell _q)$ for which the norm of 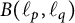${B}(\ell _p, \ell _q)$ is strongly subdifferentiable is dense in 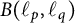${B}(\ell _p, \ell _q)$. Additionally, we present a characterization of Fréchet differentiability of the norm of bounded linear operators from 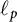$\ell _p$ to 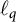$\ell _q$, where 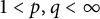$1 < p, q < \infty $. Applying this result, we will show that the Fréchet differentiability and the Gateaux differentiability of the norm of bounded linear operators on 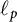$\ell _p$ spaces coincide, extending a known theorem regarding the operator norm on Hilbert spaces.

Keywords

Operators on Banach spacesFréchet and Gateaux differentiabilitystrong subdifferentiabilityℓ p spacesM-idealnorm attaining operators

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces 46B28: Spaces of operators; tensor products; approximation properties
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 20
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

A portion of this research has been supported through the JC Bose National Fellowship and grant of Prof. Debashish Goswami, sponsored by the Science and Engineering Research Board (SERB) under the Government of India.

References

Abatzoglou, T. J., Norm derivatives on spaces of operators . Math. Ann. 239(1979), no. 2, 129–135. MR519008Google Scholar
Guerrero, J. B. and Palacios, A. R., Strong subdifferentiability of the norm on ${\mathrm{JB}}^{\ast }$ -triples . Q. J. Math. 54(2003), no. 4, 381–390. MR2031171Google Scholar
Contreras, M. D., Strong subdifferentiability in spaces of vector-valued continuous functions . Quart. J. Math. Oxford Ser. (2), 47(1996), no. 186, 147–155. MR1397934Google Scholar
Contreras, M. D., Payá, R. and Werner, W., ${C}^{\ast }$ -algebras that are $I$ -rings . J. Math. Anal. Appl. 198(1996), no. 1, 227–236. MR1373537Google Scholar
Dantas, S., Jung, M., Roldán, Ó., and Zoca, A. R., Norm-attaining tensors and nuclear operators . Mediterr. J. Math. 19(2022), no. 1, 38, 27. MR4371175Google Scholar
Dantas, S., Kim, S. K., Lee, H. J., and Mazzitelli, M., Strong subdifferentiability and local Bishop-Phelps-Bollobás properties . Rev. R. Acad. Cienc. Exactas Fís. Nat. Ser. A Mat. RACSAM 114(2020), no. 2, 47, 16. MR4049872Google Scholar
Deeb, W. M. and Khalil, R. R., Exposed and smooth points of some classes of operation in $L({l}^p)$ . J. Funct. Anal, 103(1992), no. 2, 217–228. MR1151547Google Scholar
Deville, R., Godefroy, G., and Zizler, V., Smoothness and renormings in Banach spaces. Pitman Monographs and Surveys in Pure and Applied Mathematics, vol. 64, Longman Scientific & Technical, Harlow; copublished in the United States with John Wiley & Sons, Inc., New York, 1993. MR1211634Google Scholar
Diestel, J., Geometry of Banach spaces—selected topics, Springer-Verlag, Berlin, 1975. MR461094Google Scholar
Franchetti, C. and Payá, R., Banach spaces with strongly subdifferentiable norm , Boll. Un. Mat. Ital. B (7), 7(1993), no. 1, 45–70. MR1216708Google Scholar
Godefroy, G., Indumathi, V., and Lust-Piquard, F., Strong subdifferentiability of convex functionals and proximinality , J. Approx. Theory 116(2002), no. 2, 397–415. MR1911087Google Scholar
Godefroy, G., Montesinos, V., and Zizler, V., Strong subdifferentiability of norms and geometry of Banach spaces . Comment. Math. Univ. Carolin. 36(1995), no. 3, 493–502. MR1364490Google Scholar
Guerrero, J. B. and Peralta, A. M., Subdifferentiability of the norm and the Banach-Stone theorem for real and complex ${JB}^{\ast }$ -triples . Manuscripta Math. 114(2004), no. 4, 503–516. MR2081949Google Scholar
Harmand, P., Werner, D., and Werner, W., $M$ -ideals in Banach spaces and Banach algebras, Lecture Notes in Mathematics, vol. 1547, Springer-Verlag, Berlin, 1993. MR1238713Google Scholar
Kim, S. Kwang and Lee, H. J., Uniform convexity and Bishop-Phelps-Bollobás property . Canad. J. Math. 66(2014), no. 2, 373–386. MR3176146Google Scholar
Kittaneh, F. and Younis, R., Smooth points of certain operator spaces . Integral Equ. Oper. Theory 13(1990), no. 6, 849–855. MR1073855Google Scholar
Lindenstrauss, J., On operators which attain their norm . Israel J. Math. 1(1963), 139–148. MR160094Google Scholar
Martínez-Moreno, J., Mena-Jurado, J. F., Payá-Albert, R., and Rodríguez-Palacios, Á. An approach to numerical ranges without Banach algebra theory . Illinois J. Math. 29(1985), no. 4, 609–626. MR806469Google Scholar
Oja, E. and Werner, D., Remarks on $M$ -ideals of compact operators on $X{\oplus}_pX$ . Math. Nachr. 152(1991), 101–111. MR1121227Google Scholar
Pellegrino, D. and Teixeira, E. V., Norm optimization problem for linear operators in classical Banach spaces . Bull. Braz. Math. Soc. (N.S.) 40(2009), no. 3, 417–431. MR2540517Google Scholar
Rao, T. S. S. R. K., Subdifferential set of an operator . Monatsh. Math. 199(2022), no. 4, 891–898. MR4497173Google Scholar
Rao, T. S. S. R. K., Subdifferentiability and polyhedrality of the norm . Boll. Unione Mat. Ital. 16(2023), no. 4, 741–746. MR4653431Google Scholar
Ruess, W. M. and Stegall, C. P., Extreme points in duals of operator spaces . Math. Ann. 261(1982), no. 4, 535–546. MR682665Google Scholar
Ruess, W. M. and Stegall, C. P., Exposed and denting points in duals of operator spaces . Israel J. Math. 53(1986), no. 2, 163–190. MR845870Google Scholar
Ryan, R. A., Introduction to tensor products of Banach spaces, Springer Monographs in Mathematics, Springer-Verlag, London, 2002. MR1888309Google Scholar
Taylor, K. F. and Werner, W., Differentiability of the norm in von Neumann algebras . Proc. Amer. Math. Soc. 119(1993), no. 2, 475–480. MR1149980Google Scholar
Werner, W., Smooth points in some spaces of bounded operators . Integral Equ. Oper. Theory 15(1992), no. 3, 496–502. MR1155717Google Scholar