Hostname: page-component-669899f699-chc8l Total loading time: 0 Render date: 2025-05-02T06:43:57.945Z Has data issue: false hasContentIssue false
  • English
  • Français

Cyclic Groups and the Three Distance Theorem

Published online by Cambridge University Press:  20 November 2018

Nicolas Chevallier
Nicolas Chevallier*
Affiliation:
Université de Haute Alsace, 4, rue des frères Lumière, 68093 Mulhouse, France email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a two dimensional extension of the three distance theorem. Let 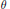$\theta $ be in 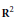${{\mathbf{R}}^{2}}$ and let $q$ be in 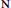$\mathbf{N}$. There exists a triangulation of 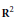${{\mathbf{R}}^{2}}$ invariant by 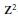${{\mathbf{Z}}^{2}}$-translations, whose set of vertices is 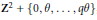${{\mathbf{Z}}^{2}}\,+\,\{0,\,\theta ,\,\ldots ,\,q\theta \}$, and whose number of different triangles, up to translations, is bounded above by a constant which does not depend on 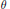$\theta $ and $q$.

Keywords

11J7011J7111J13
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 59 , Issue 3 , 01 June 2007 , pp. 503 - 552
Copyright
Copyright © Canadian Mathematical Society 2007

References

[1] Allessandri, P. and Berthé, V., Three distance theorems and combinatorics on words. Enseign. Math 44(1998), no. 1-2, 103–132.Google Scholar
[2] Babai, L., On Lovász’ lattice reduction and the nearest lattice point problem. Combinatorica 6(1986), no. 1, 1–13.Google Scholar
[3] Berthé, V. and Tijdeman, R., Balance properties of multi-dimensional words. Theoret. Comput. Sci. 273(2002), no. 1-2, 197–224.Google Scholar
[4] Boot, B., Okabe, A., and Sugihara, K., Spatial Tessellations, Concepts and Applications of Voronoï Diagrams. John Wiley, 1991.Google Scholar
[5] Chevallier, N., Meilleures approximations d’un élément du tore T2 et géométrie de la suite des multiples de cet élément. Acta Arith. 78(1996), no. 1, 19–35.Google Scholar
[6] Chevallier, N., Géométrie des suites de Kronecker. Manuscripta Math. 94(1997), no. 2, 231–241.Google Scholar
[7] Chevallier, N., Three distance theorem and grid graph. Discrete Math. 223(2000), no. 1-3, 355–362.Google Scholar
[8] Chevallier, N., Meilleures approximations diophantiennes d’un élément du tore T d. Acta Arith. 97(2001), no. 3, 219–240.Google Scholar
[9] Chung, F. R. K. and Graham, R. L., On the set of distances determined by union of arithmetic progression. Ars. Combinatoria 1(1976), no. 1, 57–76.Google Scholar
[10] Dieudonné, J., Éléments d’analyse. I. fondements de l’analyse moderne. Gauthier-Villars, Paris, 1972.Google Scholar
[11] Drmota, M. and Tichy, R., Sequences, Discrepancies and Applications. Lectures Notes in Mathematics 1651, Springer-Verlag, Berlin, 1997.Google Scholar
[12] Fried, E. and Sós, V. T., A generalization of the three-distance theorem for groups. Algebra Universalis, 29(1992), no. 1, 136–149.Google Scholar
[13] Grötschel, M., Lovász, L., and Schrijver, A., Geometric Algorithms and Combinatorial Optimization. Second edition. Algorithms and Combinatorics 2, Springer-Verlag, Berlin, 1993.Google Scholar
[14] Geelen, A. S. and Simpson, R. J., A two dimensional Steinhaus theorem. Australas. J. Combin. 8 (1993), 136–197.Google Scholar
[15] Lagarias, J. C., Some new results in simultaneous Diophantine approximation. Proc. of the Queen's Number Theory Conference 1979 (Ribenboim, P., Ed.), Queen's Paper in Pure and Applied Math. No. 54 (1980), 453–474.Google Scholar
[16] Lagarias, J. C., Best simultaneous Diophantine approximations I. Growth Rates of Best Approximations denominators, Trans. Amer. Math. Soc. 272(1982), no. 2, 545–554.Google Scholar
[17] Lagarias, J. C., Best simultaneous Diophantine approximations II. Behavior of consecutive best approximations. Pacific J. Math. 102(1982), no. 1, 61–88.Google Scholar
[18] Lagarias, J. C., Best Diophantine approximations to a set of linear forms. J. Austral. Math. Soc. Ser. A 34(1983), no. 1, 114–122.Google Scholar
[19] Lagarias, J. C., The computational complexity of simultaneous Diophantine approximations problems. SIAM J. Comput. 14(1985), no. 1, 196–209.Google Scholar
[20] Lagarias, J. C., Geodesic multidimensional continued fractions. Proc. London Math. Soc. 69(1994), no. 3, 464–488.Google Scholar
[21] Langevin, M., Stimulateur cardiaque et suite de Farey. Period. Math. Hungar. 23(1991), no. 1, 75–86.Google Scholar
[22] Liang, F. M., A short proof of the 3d distance theorem. Discrete Math. 28 (1979), no. 3, 325–326.Google Scholar
[23] Mignosi, F., On the number of factors of Sturmian words. Theoret. Comput. Sci. 82(1991), no. 1, 71–84.Google Scholar
[24] Preparata, F. P. and Shamos, M. I., Computational geometry. An Introduction. Texts and Monographs in Computer Science, Springer-Verlag, New York, 1985.Google Scholar
[25] Pytheas Fogg, N., Substitutions in Dynamics, Arithmetic and Combinatorics. Lectures Notes in Mathematics 1794, Springer-Verlag, Berlin, 2002.Google Scholar
[26] van Ravenstein, T., Three gap theorem (Steinhaus conjecture). J. Austral. Math. Soc. Ser. a 45(1988), no. 3, 360–370.Google Scholar
[27] Rogers, C. A., The signatures of the errors of some simultaneous Diophantine approximations. Proc. London Math. Soc. 52(1951), 186–190.Google Scholar
[28] Siegel, A., Théorème des trois longueurs et suites sturmiennes: mots d’agencement des longueurs. Acta Arith. 97(2001), no. 3, 195–210.Google Scholar
[29] Slater, N. B., The distribution of the integers N for whic. ﹛θN﹜ < ϕ. Proc. Cambridge Philos. Soc. 46(1950), 525–534.Google Scholar
[30] Slater, N. B., Distribution problems and physical applications. Compositio Math. 16(1964), 176–183.Google Scholar
[31] Slater, N. B., Gaps and steps for the sequence nθ. mod 1. Proc. Cambridge Philos. Soc. 63(1967), 1115–1123.Google Scholar
[32] Sós, V. T., On the theory of diophantine approximation. I. Acta Math. Acad. Sci. Hung. 8(1957), 461–472.Google Scholar
[33] Sós, V. T., On the theory of Diophantine approximation. II. Acta Math. Acad. Sci. Hung. 9(1958), 229–241.Google Scholar
[34] Sós, V. T., On the distribution mod 1 of the sequence nα, Ann. Univ. Sci. Budapest, Eötvös Sect. Math. 1 (1958), 127–134.Google Scholar
[35] Świerczkowski, S., On the successive settings of an arc on the circumference of a circle. Fund. Math. 46(1959), 187–189.Google Scholar