Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-29T20:49:28.507Z Has data issue: false hasContentIssue false
  • English
  • Français

Convolution of periodic multiplicative functions and the divisor problem

Part of: Multiplicative number theory

Published online by Cambridge University Press:  14 November 2024

Marco Aymone ,
Gopal Maiti ,
Olivier Ramaré Open the ORCID record for Olivier Ramaré [Opens in a new window]  and
Priyamvad Srivastav
Marco Aymone*
Affiliation:
Universidade Federal de Minas Gerais (UFMG), Belo Horizonte, Brazil
Gopal Maiti
Affiliation:
Max Planck Institute for Mathematics (MPIM), Bonn, Germany e-mail: [email protected]
Olivier Ramaré
Affiliation:
CNRS / Aix-Marseille Université, Marseille, France e-mail: [email protected]
Priyamvad Srivastav
Affiliation:
Mumbai, India e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study a certain class of arithmetic functions that appeared in Klurman’s classification of 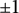$\pm 1$ multiplicative functions with bounded partial sums; c.f., Comp. Math. 153(2017), 2017, no. 8, 1622–1657. These functions are periodic and 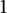$1$-pretentious. We prove that if 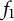$f_1$ and 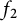$f_2$ belong to this class, then 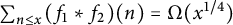$\sum _{n\leq x}(f_1\ast f_2)(n)=\Omega (x^{1/4})$. This confirms a conjecture by the first author. As a byproduct of our proof, we studied the correlation between 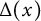$\Delta (x)$ and 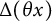$\Delta (\theta x)$, where 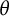$\theta $ is a fixed real number. We prove that there is a nontrivial correlation when 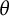$\theta $ is rational, and a decorrelation when 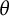$\theta $ is irrational. Moreover, if 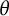$\theta $ has a finite irrationality measure, then we can make it quantitative this decorrelation in terms of this measure.

Keywords

Dirichlet divisor problemcorrelations in the divisor problemomega boundsperiodic multiplicative functions

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Type
Article
Information
Canadian Journal of Mathematics , First View , pp. 1 - 19
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The visit of the first author to the Aix-Marseille Université was funded by CNPq grant PDE no. 400010/2022-4 (200121/2022-7). His research also is supported by FAPEMIG, grant Universal no. APQ-00256-23 and by CNPq grant Universal no. 403037/2021-2. The second and third author are supported by the joint FWF-ANR project Arithrand: FWF: I 4945-N and ANR-20-CE91-0006.

References

Aymone, M., Complex valued multiplicative functions with bounded partial sums . Bull. Braz. Math. Soc. (N.S.) 53(2022), 1317–1329.CrossRefGoogle Scholar
Báez-Duarte, L., Balazard, M., Landreau, B. and Saias, E., Étude de l’autocorrélation multiplicative de la fonction ‘partie fractionnaire’ . Ramanujan J. 9(2005), 215–240.CrossRefGoogle Scholar
Balazard, M. and Martin, B., Sur l’autocorrélation multiplicative de la fonction partie fractionnaire et une fonction définie par J. R. Wilton. https://hal.archives-ouvertes.fr/hal-00823899v1, (2013).Google Scholar
Balazard, M. and Martin, B., Sur une équation fonctionnelle approchée due à J. R. Wilton . Mosc. Math. J. 15(2015), 629–652.CrossRefGoogle Scholar
Borda, B., Munsch, M. and Shparlinski, I. E., Pointwise and correlation bounds on Dedekind sums over small subgroups . Res. Number Theory 10(2024), Paper No. 28, 12.CrossRefGoogle Scholar
Coons, M., On the multiplicative Erdös discrepancy problem. Preprint, 2010, arXiv:1003.5388.Google Scholar
Erdős, P., Some unsolved problems . Michigan Math. J. 4(1957), 291–300.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., Pretentious multiplicative functions and an inequality for the zeta-function . In Anatomy of integers, CRM Proc. Lecture Notes, Vol. 46, Amer. Math. Soc., Providence, RI, 2008, 191–197.Google Scholar
Huxley, M. N., Exponential sums and lattice points. III . Proc. London Math. Soc. (3) 87(2003), 591–609.CrossRefGoogle Scholar
Ivić, A. and Zhai, W., On certain integrals involving the Dirichlet divisor problem . Funct. Approx. Comment. Math. 62(2020), 247–267.CrossRefGoogle Scholar
Khintchine, A., Einige Sätze über Kettenbrüche, mit Anwendungen auf die Theorie der Diophantischen Approximationen . Math. Ann. 92(1924), 115–125.CrossRefGoogle Scholar
Klurman, O., Correlations of multiplicative functions and applications . Compos. Math. 153(2017), 1622–1657.CrossRefGoogle Scholar
Lau, Y.-K. and Tsang, K.-M., Mean square of the remainder term in the Dirichlet divisor problem . In Les Dix-huitièmes Journées Arithmétiques (Bordeaux, 1993), Vol. 7, 1995, 75–92.Google Scholar
Lee, S. H. and Lee, S., The twisted moments and distribution of values of Dirichlet $L$ -functions at 1. J. Number Theory 197(2019), 168–184.CrossRefGoogle Scholar
Nyman, B., On the one-dimensional translation group and semi-group in certain function spaces, Thesis, University of Uppsala, Uppsala, 1950.Google Scholar
Soundararajan, K., Omega results for the divisor and circle problems . Int. Math. Res. Not. (2003), 1987–1998.CrossRefGoogle Scholar
Tao, T., The Erdös discrepancy problem . Discrete Anal. (2016), Paper No. 1, 29.CrossRefGoogle Scholar
Tong, K.-C., On divisor problems. II, III . Acta Math. Sinica 6(1956), 139–152, 515–541.Google Scholar