Hostname: page-component-669899f699-qzcqf Total loading time: 0 Render date: 2025-04-26T22:49:17.446Z Has data issue: false hasContentIssue false
  • English
  • Français

SYMMETRIC ITINERARY SETS

Part of: Classical measure theory Topological dynamics

Published online by Cambridge University Press:  06 March 2019

MICHAEL F. BARNSLEY  and
NICOLAE MIHALACHE
MICHAEL F. BARNSLEY*
Affiliation:
Department of Mathematics, Australian National University, Canberra, ACT, Australia email [email protected]
NICOLAE MIHALACHE
Affiliation:
Université Paris-Est Créteil, LAMA, 94 010 Créteil, France email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider a one-parameter family of dynamical systems 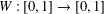$W:[0,1]\rightarrow [0,1]$ constructed from a pair of monotone increasing diffeomorphisms 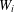$W_{i}$ such that 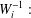$W_{i}^{-1}:$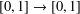$[0,1]\rightarrow [0,1]$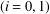$(i=0,1)$. We characterise the set of symbolic itineraries of 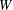$W$ using an attractor 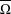$\overline{\unicode[STIX]{x1D6FA}}$ of an iterated closed relation, in the terminology of McGehee, and prove that there is a member of the family for which 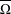$\overline{\unicode[STIX]{x1D6FA}}$ is symmetrical.

Keywords

dynamical systemsintervalitinerary

MSC classification

Primary: 37B10: Symbolic dynamics
Secondary: 28A80: Fractals 37B40: Topological entropy
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 100 , Issue 1 , August 2019 , pp. 97 - 108
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Barnsley, M. F., Harding, B. and Igudesman, K., ‘How to filter and transform images using iterated function systems’, SIAM J. Imaging Sci. 4 (2011), 1001–1024.Google Scholar
Harding, B., ‘Symmetric itinerary sets—algorithms and non-linear examples’, Bull. Aust. Math. Soc. (2019), to appear.Google Scholar
Igudesman, K. B., ‘A certain family of self-similar sets’, Russian Math. (Iz. VUZ) 55 (2011), 26–38.Google Scholar
McGehee, R. P. and Wiandt, T., ‘Conley decomposition for closed relations’, Differ. Equ. Appl. 12 (2006), 1–47.Google Scholar
Parry, W., ‘Symbolic dynamics and transformations of the unit interval’, Trans. Amer. Math. Soc. 122 (1966), 368–378.Google Scholar