Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-29T20:48:07.108Z Has data issue: false hasContentIssue false
  • English
  • Français

SOLVABLE GROUPS WHOSE NONNORMAL SUBGROUPS HAVE FEW ORDERS

Part of: Representation theory of groups

Published online by Cambridge University Press:  27 December 2023

LIJUAN HE Open the ORCID record for LIJUAN HE [Opens in a new window] ,
HENG LV Open the ORCID record for HENG LV [Opens in a new window]  and
GUIYUN CHEN Open the ORCID record for GUIYUN CHEN [Opens in a new window]
LIJUAN HE
Affiliation:
School of Mathematics and Statistics, Southwest University, Chongqing 400715, P. R. China e-mail: [email protected]
HENG LV*
Affiliation:
School of Mathematics and Statistics, Southwest University, Chongqing 400715, P. R. China
GUIYUN CHEN
Affiliation:
School of Mathematics and Statistics, Southwest University, Chongqing 400715, P. R. China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Suppose that G is a finite solvable group. Let 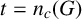$t=n_c(G)$ denote the number of orders of nonnormal subgroups of G. We bound the derived length 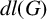$dl(G)$ in terms of 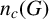$n_c(G)$. If G is a finite p-group, we show that 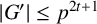$|G'|\leq p^{2t+1}$ and 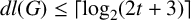$dl(G)\leq \lceil \log _2(2t+3)\rceil $. If G is a finite solvable nonnilpotent group, we prove that the sum of the powers of the prime divisors of 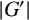$|G'|$ is less than t and that 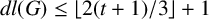$dl(G)\leq \lfloor 2(t+1)/3\rfloor +1$.

Keywords

solvable groupsnonnormal subgroupsderived length

MSC classification

Primary: 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 1 , August 2024 , pp. 121 - 128
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This research is supported by the National Natural Science Foundation of China (Nos. 11971391, 12071376), by Fundamental Research Funds for the Central Universities (SWU-XDJH202305) and the Postgraduate Research and Innovation Project of Southwest University (SWUB23034).

References

An, L. J., ‘Finite $p$ -groups whose non-normal subgroups have few orders’, Front. Math. China 13(4) (2018), 763–777.Google Scholar
Berkovich, Y., Groups of Prime Power Order, De Gruyter Expositions in Mathematics, 1 (Walter de Gruyter, Berlin, 2008).Google Scholar
Brandl, R., ‘Groups with few non-normal subgroups’, Comm. Algebra 23(6) (1995), 2091–2098.Google Scholar
Brandl, R., ‘Non-soluble groups with few conjugacy classes of non-normal subgroups’, Beitr. Algebra Geom. 54(2) (2013), 493–501.Google Scholar
Chen, G. Y. and Chen, S. M., ‘A note on the solvability of a finite group and the number of conjugate classes of its non-normal subgroups’, Southeast Asian Bull. Math. 34(4) (2010), 625–628.Google Scholar
Dedekind, R., ‘Üeber Gruppen, deren sämmtliche Theiler Normaltheiler sind’, Math. Ann. 48 (1897), 548–561.CrossRefGoogle Scholar
Gong, L., Cao, H. P. and Chen, G. Y., ‘Finite nilpotent groups having exactly four conjugacy classes of non-normal subgroups’, Algebra Colloq. 20(4) (2013), 579–592.Google Scholar
Kurzweil, H. and Stellmacher, B., The Theory of Finite Groups. An Introduction, Universitext (Springer-Verlag, New York, 2004); translated from the 1998 German original.Google Scholar
Mousavi, H., ‘On finite groups with few non-normal subgroups’, Comm. Algebra 27(7) (1999), 3143–3151.CrossRefGoogle Scholar
Mousavi, H., ‘Nilpotent groups with three conjugacy classes of non-normal subgroups’, Bull. Iranian Math. Soc. 40(5) (2014), 1291–1300.Google Scholar
Mousavi, H., ‘Non-nilpotent groups with three conjugacy classes of non-normal subgroups’, Int. J. Group Theory 3(2) (2014), 1–7.Google Scholar
Passman, D. S., ‘Nonnormal subgroups of $p$ -groups’, J. Algebra 15 (1970), 352–370.Google Scholar
Zhang, J. Q., ‘Finite groups all of whose non-normal subgroups possess the same order’, J. Algebra Appl. 11(3) (2012), Article no. 1250053, 7 pages.CrossRefGoogle Scholar