Hostname: page-component-669899f699-7xsfk Total loading time: 0 Render date: 2025-05-02T11:16:42.282Z Has data issue: false hasContentIssue false
  • English
  • Français

RADICALS AND IDEMPOTENTS III: q-CENTRAL IDEMPOTENTS

Part of: Radicals and radical properties of rings

Published online by Cambridge University Press:  20 November 2024

E. P. COJUHARI Open the ORCID record for E. P. COJUHARI [Opens in a new window]  and
B. J. GARDNER Open the ORCID record for B. J. GARDNER [Opens in a new window]
E. P. COJUHARI*
Affiliation:
Department of Mathematics, Technical University of Moldova, Chişinău, Moldova
B. J. GARDNER
Affiliation:
Discipline of Mathematics, University of Tasmania, Hobart, Australia e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Previously [‘Radicals and idempotents I, II’, Comm. Alg. 49(1) (2021), 73–84 and 50(11) (2022), 4791–4804], we have studied the interaction between radicals of rings and idempotents in general or those of particular types, for example, left semicentral. Here we carry out similar investigations for q-central idempotents, that is, those idempotents e satisfying the condition 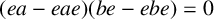$(ea-eae)(be-ebe) = 0$ for all a, b.

Keywords

cornerradical classsemi-simple class

MSC classification

Primary: 16N80: General radicals and rings
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 272 - 282
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Anh, P. N., Birkenmeier, G. F. and van Wyk, L., ‘Peirce decompositions, idempotents and rings’, J. Algebra 564 (2020), 247–275.CrossRefGoogle Scholar
Cojuhari, E. P. and Gardner, B. J., ‘Radicals and idempotents I’, Comm. Algebra 49(1) (2021), 73–84.CrossRefGoogle Scholar
Cojuhari, E. P. and Gardner, B. J., ‘Radicals and idempotents II’, Comm. Algebra 50(11) (2022), 4791–4804.CrossRefGoogle Scholar
Gardner, B. J. and Wiegandt, R., Radical Theory of Rings (Marcel Dekker, New York–Basel, 2004).Google Scholar
Lam, T. Y., ‘An introduction to $q$ -central idempotents and $q$ -abelian rings’, Comm. Algebra 51(3) 2023), 1071–1088.CrossRefGoogle Scholar