Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-29T23:43:00.093Z Has data issue: false hasContentIssue false
  • English
  • Français

PARITY RESULTS FOR PARTITIONS WHEREIN EACH PART APPEARS AN ODD NUMBER OF TIMES

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  12 November 2018

MICHAEL D. HIRSCHHORN  and
JAMES A. SELLERS
MICHAEL D. HIRSCHHORN
Affiliation:
School of Mathematics and Statistics, UNSW, Sydney 2052, Australia email [email protected]
JAMES A. SELLERS*
Affiliation:
Department of Mathematics, Penn State University, University Park, PA 16802, USA email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the function 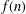$f(n)$ that enumerates partitions of weight $n$ wherein each part appears an odd number of times. Chern [‘Unlimited parity alternating partitions’, Quaest. Math. (to appear)] noted that such partitions can be placed in one-to-one correspondence with the partitions of $n$ which he calls unlimited parity alternating partitions with smallest part odd. Our goal is to study the parity of 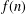$f(n)$ in detail. In particular, we prove a characterisation of 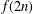$f(2n)$ modulo 2 which implies that there are infinitely many Ramanujan-like congruences modulo 2 satisfied by the function 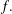$f.$ The proof techniques are elementary and involve classical generating function dissection tools.

Keywords

congruencespartitionsgenerating functions

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 51 - 55
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

References

Andrews, G. E., ‘Ramanujan’s “Lost” notebook, IV. Stacks and alternating parity in partitions’, Adv. Math. 53(1) (1984), 55–74.Google Scholar
Chern, S., ‘Unlimited parity alternating partitions’, Quaest. Math., to appear.Google Scholar
Hirschhorn, M. D., The Power of q , Developments in Mathematics, 49 (Springer, Cham, Switzerland, 2017).Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Elementary proofs of various facts about 3-cores’, Bull. Aust. Math. Soc. 79 (2009), 507–512.Google Scholar