Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-05-01T04:27:22.503Z Has data issue: false hasContentIssue false
  • English
  • Français

OVERGROUPS OF WEAK SECOND MAXIMAL SUBGROUPS

Part of: Representation theory of groups

Published online by Cambridge University Press:  30 August 2018

HANGYANG MENG Open the ORCID record for HANGYANG MENG [Opens in a new window]  and
XIUYUN GUO Open the ORCID record for XIUYUN GUO [Opens in a new window]
HANGYANG MENG*
Affiliation:
Department of Mathematics, Shanghai University, Shanghai 200444, PR China email [email protected]
XIUYUN GUO
Affiliation:
Department of Mathematics, Shanghai University, Shanghai 200444, PR China email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A subgroup 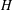$H$ is called a weak second maximal subgroup of 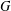$G$ if 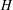$H$ is a maximal subgroup of a maximal subgroup of 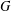$G$. Let 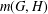$m(G,H)$ denote the number of maximal subgroups of 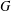$G$ containing 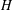$H$. We prove that 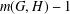$m(G,H)-1$ divides the index of some maximal subgroup of 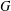$G$ when 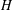$H$ is a weak second maximal subgroup of 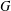$G$. This partially answers a question of Flavell [‘Overgroups of second maximal subgroups’, Arch. Math.64(4) (1995), 277–282] and extends a result of Pálfy and Pudlák [‘Congruence lattices of finite algebras and intervals in subgroup lattices of finite groups’, Algebra Universalis11(1) (1980), 22–27].

Keywords

weak second maximal subgroupsmaximal subgroupscompletely reducible modules

MSC classification

Primary: 20D30: Series and lattices of subgroups
Secondary: 20C05: Group rings of finite groups and their modules 20D10: Solvable groups, theory of formations, Schunck classes, Fitting classes, $pi$-length, ranks
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 83 - 88
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The research for this work was partially supported by the National Natural Science Foundation of China (11771271).

References

Flavell, P., ‘Overgroups of second maximal subgroups’, Arch. Math. 64(4) (1995), 277–282.Google Scholar
Gorenstein, D., Finite Groups (Harper and Row–Collier-Macmillan, New York, 1968).Google Scholar
Huppert, B., Endliche Gruppen I (Springer, Berlin–Heidelberg, 1967).Google Scholar
Meng, H. and Guo, X., ‘Weak second maximal subgroups in solvable groups’, arXiv:1808.02309.Google Scholar
Pálfy, P. P. and Pudlák, P., ‘Congruence lattices of finite algebras and intervals in subgroup lattices of finite groups’, Algebra Universalis 11(1) (1980), 22–27.Google Scholar