Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-29T23:35:27.784Z Has data issue: false hasContentIssue false
  • English
  • Français

ON THE EXCEPTIONAL SET OF TRANSCENDENTAL ENTIRE FUNCTIONS IN SEVERAL VARIABLES

Part of: Holomorphic functions of several complex variables Diophantine approximation, transcendental number theory

Published online by Cambridge University Press:  20 October 2023

DIEGO ALVES Open the ORCID record for DIEGO ALVES [Opens in a new window] ,
JEAN LELIS Open the ORCID record for JEAN LELIS [Opens in a new window] ,
DIEGO MARQUES Open the ORCID record for DIEGO MARQUES [Opens in a new window]  and
PAVEL TROJOVSKÝ Open the ORCID record for PAVEL TROJOVSKÝ [Opens in a new window]
DIEGO ALVES
Affiliation:
Instituto Federal do Ceará, Crateús, CE, Brazil e-mail: [email protected]
JEAN LELIS*
Affiliation:
Faculdade de Matemática/ICEN/UFPA, Belém, PA, Brazil
DIEGO MARQUES
Affiliation:
Departamento De Matemática, Universidade De Brasília, Brasília, DF, Brazil e-mail: [email protected]
PAVEL TROJOVSKÝ
Affiliation:
Faculty of Science, University of Hradec Králové, Hradec Králové, Czech Republic e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that any subset of 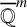$\overline {\mathbb {Q}}^m$ (closed under complex conjugation and which contains the origin) is the exceptional set of uncountably many transcendental entire functions over 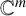$\mathbb {C}^m$ with rational coefficients. This result solves a several variables version of a question posed by Mahler for transcendental entire functions [Lectures on Transcendental Numbers, Lecture Notes in Mathematics, 546 (Springer-Verlag, Berlin, 1976)].

Keywords

exceptional setalgebraictranscendentaltranscendental functions of several variables

MSC classification

Primary: 11J81: Transcendence (general theory)
Secondary: 32A15: Entire functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 1 , August 2024 , pp. 64 - 71
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

Diego Marques was supported by CNPq-Brazil. Pavel Trojovský was supported by the Project of Excellence, Faculty of Science, University of Hradec Králové, No. 2210/2023-2024.

References

Mahler, K., Lectures on Transcendental Numbers, Lecture Notes in Mathematics, 546 (Springer-Verlag, Berlin, 1976).Google Scholar
Marques, D. and Moreira, C. G., ‘A note on a complete solution of a problem posed by Mahler’, Bull. Aust. Math. Soc. 98(1) (2018), 60–63.Google Scholar
Marques, D. and Ramirez, J., ‘On exceptional sets: the solution of a problem posed by K. Mahler’, Bull. Aust. Math. Soc. 94 (2016), 15–19.Google Scholar
Stäckel, P., ‘Ueber arithmetische Eingenschaften analytischer Functionen’, Math. Ann. 46 (1895), 513–520.Google Scholar
Waldschmidt, M., ‘Algebraic values of analytic functions’, J. Comput. Appl. Math. 160 (2003), 323–333.Google Scholar