Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-04-29T19:41:29.008Z Has data issue: false hasContentIssue false
  • English
  • Français

ON SUMS INVOLVING THE EULER TOTIENT FUNCTION

Part of: Elementary number theory Multiplicative number theory

Published online by Cambridge University Press:  24 August 2023

ISAO KIUCHI  and
YUKI TSURUTA
ISAO KIUCHI
Affiliation:
Department of Mathematical Sciences, Faculty of Science, Yamaguchi University, Yoshida 1677-1, Yamaguchi 753-8512, Japan e-mail: [email protected]
YUKI TSURUTA*
Affiliation:
Graduate School of Engineering, Oita University, 700 Dannoharu, Oita 870–1192, Japan
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

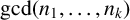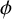Let $\gcd (n_{1},\ldots ,n_{k})$ denote the greatest common divisor of positive integers $n_{1},\ldots ,n_{k}$ and let $\phi $ be the Euler totient function. For any real number 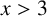$x>3$ and any integer 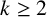$k\geq 2$, we investigate the asymptotic behaviour of 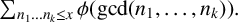$\sum _{n_{1}\ldots n_{k}\leq x}\phi (\gcd (n_{1},\ldots ,n_{k})). $

Keywords

gcd-sum functionEuler totient functionDirichlet seriesdivisor functionLindelöf hypothesisasymptotic results on arithmetical functions

MSC classification

Primary: 11N37: Asymptotic results on arithmetic functions
Secondary: 11A25: Arithmetic functions; related numbers; inversion formulas
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 109 , Issue 3 , June 2024 , pp. 486 - 497
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The first author is supported by JSPS Grant-in-Aid for Scientific Research (C)(21K03205).

References

Bourgain, J., ‘Decoupling, exponential sums and the Riemann zeta-function’, J. Amer. Math. Soc. 30 (2017), 205–224.CrossRefGoogle Scholar
Graham, S. W. and Kolesnik, G., Van der Corput’s Method of Exponential Sums, London Mathematical Society Lecture Note Series, 126 (Cambridge University Press, Cambridge, 1991).CrossRefGoogle Scholar
Heyman, R. and Tóth, L., ‘Hyperbolic summation for functions of the GCD and LCM of several integers’, Ramanujan J., to appear. Published online (28 December 2022).CrossRefGoogle Scholar
Huxley, M. N., ‘Exponential sums and lattice points. III’, Proc. Lond. Math. Soc. (3) 87 (2003), 591–609.CrossRefGoogle Scholar
Huxley, M. N., ‘Exponential sums and the Riemann zeta-function. V’, Proc. Lond. Math. Soc. (3) 90 (2005), 1–40.CrossRefGoogle Scholar
Huxley, M. N. and Watt, N., ‘Exponential sums and the Riemann zeta-function’, Proc. Lond. Math. Soc. (3) 57 (1988), 1–24.CrossRefGoogle Scholar
Ivić, A., The Riemann Zeta-Function: Theory and Applications (Dover, Mineola, NY, 1985).Google Scholar
Kiuchi, I. and Saad Eddin, S., ‘On sums of arithmetic functions involving the greatest common divisor’, Preprint, 2021, arxiv:2102.03714v1.Google Scholar
Krätzel, E., Lattice Points, Mathematics and its Applications. East European Series, 33 (Kluwer, Dordrecht, 1988).Google Scholar
Krätzel, E., Nowak, W. G. and Tóth, L., ‘On certain arithmetic functions involving the greatest common divisor’, Cent. Eur. J. Math. 10 (2012), 761–774.Google Scholar
Kühleitner, M. and Nowak, W. G., ‘On a question of A. Schinzel: omega estimate for a special type of arithmetic functions’, Cent. Eur. J. Math. 11 (2013), 477–486.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Multiplicative Number Theory I. Classical Theory, Cambridge Studies in Advanced Mathematics, 97 (Cambridge University Press, Cambridge, 2007).Google Scholar
Tenenbaum, G., Introduction to Analytic and Probabilistic Number Theory, Graduate Studies in Mathematics, 163 (American Mathematical Society, Providence, RI, 2008).Google Scholar
Titchmarsh, E. C., The Theory of the Riemann Zeta-function, revised by D. R. Heath-Brown (Oxford University Press, Oxford, 1986).Google Scholar