Hostname: page-component-669899f699-7tmb6 Total loading time: 0 Render date: 2025-05-01T21:24:09.673Z Has data issue: false hasContentIssue false
  • English
  • Français

ON MAXIMALLY FROBENIUS DESTABILISED VECTOR BUNDLES

Part of: Families, fibrations Arithmetic problems. Diophantine geometry Curves

Published online by Cambridge University Press:  04 January 2019

LINGGUANG LI Open the ORCID record for LINGGUANG LI [Opens in a new window]
LINGGUANG LI*
Affiliation:
School of Mathematical Sciences, Tongji University, Shanghai, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 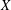$X$ be a smooth projective curve of genus 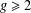$g\geq 2$ over an algebraically closed field 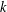$k$ of characteristic 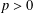$p>0$. We show that for any integers $r$ and 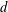$d$ with 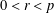$0<r<p$, there exists a maximally Frobenius destabilised stable vector bundle of rank $r$ and degree 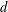$d$ on 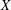$X$ if and only if 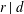$r\mid d$.

Keywords

vector bundlemoduli spaceFrobenius morphism

MSC classification

Primary: 14H60: Vector bundles on curves and their moduli
Secondary: 14D20: Algebraic moduli problems, moduli of vector bundles 14D22: Fine and coarse moduli spaces 14G17: Positive characteristic ground fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 2 , April 2019 , pp. 195 - 202
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

Footnotes

This work was supported by the National Natural Science Foundation of China (Grant No. 11501418) and the Shanghai Sailing Program (15YF1412500).

References

Hirschowitz, A., ‘Probléme de Brill–Noether en rang supérieur’, C. R. Acad. Sci. Paris 307 (1988), 153–156.Google Scholar
Joshi, K., ‘The degree of the dormant operatic locus’, Int. Math. Res. Not. IMRN 2017(9) (2017), 2599–2613.Google Scholar
Joshi, K. and Pauly, C., ‘Hitchin–Mochizuki morphism, opers and Frobenius-destabilized vector bundles over curves’, Adv. Math. 274 (2015), 39–75.Google Scholar
Joshi, K., Ramanan, S., Xia, E. Z. and Yu, J.-K., ‘On vector bundles destabilized by Frobenius pull-back’, Compos. Math. 142 (2006), 616–630.Google Scholar
Li, L., ‘The morphism induced by Frobenius push-forward’, Sci. China Math. 57(1) (2014), 61–67.Google Scholar
Mochizuki, S., ‘A theory of ordinary p-adic curves’, Publ. Res. Inst. Math. Sci. 32(6) (1996), 957–1152.Google Scholar
Mochizuki, S., Foundations of p-adic Teichmüller theory, AMS/IP Studies in Advanced Mathematics, 11 (American Mathematical Society, Providence, RI, 1999).Google Scholar
Osserman, B., ‘Frobenius-unstable bundles and p-curvature’, Trans. Amer. Math. Soc. 360(1) (2008), 273–305.Google Scholar
Sun, X., ‘Direct images of bundles under Frobenius morphisms’, Invent. Math. 173(2) (2008), 427–447.Google Scholar
Sun, X., ‘Stability of sheaves of locally closed and exact forms’, J. Algebra 324 (2010), 1471–1482.Google Scholar
Zhao, Y., ‘Maximally Frobenius-destabilized vector bundles over smooth algebraic curves’, Internat. J. Math. 28(2) (2017), Article ID 1750003, 26 pages.Google Scholar