Motivated by the work initiated by Chapman [‘Determinants of Legendre symbol matrices’, Acta Arith. 115 (2004), 231–244], we investigate some arithmetical properties of generalised Legendre matrices over finite fields. For example, letting 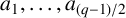$a_1,\ldots ,a_{(q-1)/2}$ be all the nonzero squares in the finite field 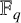$\mathbb {F}_q$ containing q elements with 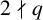$2\nmid q$, we give the explicit value of the determinant 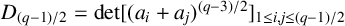$D_{(q-1)/2}=\det [(a_i+a_j)^{(q-3)/2}]_{1\le i,j\le (q-1)/2}$. In particular, if 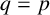$q=p$ is a prime greater than 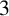$3$, then

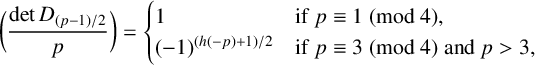$$ \begin{align*}\bigg(\frac{\det D_{(p-1)/2}}{p}\bigg)= \begin{cases} 1 & \mbox{if}\ p\equiv1\pmod4,\\ (-1)^{(h(-p)+1)/2} & \mbox{if}\ p\equiv 3\pmod4\ \text{and}\ p>3, \end{cases}\end{align*} $$

where 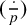$(\frac {\cdot }{p})$ is the Legendre symbol and 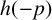$h(-p)$ is the class number of 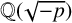$\mathbb {Q}(\sqrt {-p})$.