Published online by Cambridge University Press: 21 November 2023
Let 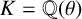 $K={\mathbb {Q}}(\theta )$ be an algebraic number field with
$K={\mathbb {Q}}(\theta )$ be an algebraic number field with 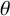 $\theta $ satisfying a monic irreducible polynomial
$\theta $ satisfying a monic irreducible polynomial 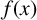 $f(x)$ of degree n over
$f(x)$ of degree n over 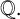 ${\mathbb {Q}}.$ The polynomial
${\mathbb {Q}}.$ The polynomial 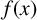 $f(x)$ is said to be monogenic if
$f(x)$ is said to be monogenic if  $\{1,\theta ,\ldots ,\theta ^{n-1}\}$ is an integral basis of K. Deciding whether or not a monic irreducible polynomial is monogenic is an important problem in algebraic number theory. In an attempt to answer this problem for a certain family of polynomials, Jones [‘A brief note on some infinite families of monogenic polynomials’, Bull. Aust. Math. Soc. 100 (2019), 239–244] conjectured that if
$\{1,\theta ,\ldots ,\theta ^{n-1}\}$ is an integral basis of K. Deciding whether or not a monic irreducible polynomial is monogenic is an important problem in algebraic number theory. In an attempt to answer this problem for a certain family of polynomials, Jones [‘A brief note on some infinite families of monogenic polynomials’, Bull. Aust. Math. Soc. 100 (2019), 239–244] conjectured that if 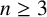 $n\ge 3$,
$n\ge 3$, 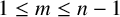 $1\le m\le n-1$,
$1\le m\le n-1$, 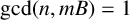 $\gcd (n,mB)=1$ and A is a prime number, then the polynomial
$\gcd (n,mB)=1$ and A is a prime number, then the polynomial 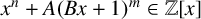 $x^n+A (Bx+1)^m\in {\mathbb {Z}}[x]$ is monogenic if and only if
$x^n+A (Bx+1)^m\in {\mathbb {Z}}[x]$ is monogenic if and only if 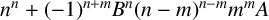 $n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA$ is square-free. We prove that this conjecture is true.
$n^n+(-1)^{n+m}B^n(n-m)^{n-m}m^mA$ is square-free. We prove that this conjecture is true.
The first author is grateful to the Council of Scientific and Industrial Research, New Delhi for providing financial support in the form of Senior Research Fellowship through Grant No. 09/135(0878)/2019-EMR-1.
The second author is grateful to the University Grants Commission, New Delhi, for providing financial support in the form of Senior Research Fellowship through Ref No.1129/(CSIR-NET JUNE 2019).