Hostname: page-component-669899f699-cf6xr Total loading time: 0 Render date: 2025-04-28T09:55:40.663Z Has data issue: false hasContentIssue false
  • English
  • Français

A NOTE ON THE FINITELY GENERATED FIXED SUBGROUP PROPERTY

Part of: Special aspects of infinite or finite groups Low-dimensional topology

Published online by Cambridge University Press:  11 October 2024

JIALIN LEI Open the ORCID record for JIALIN LEI [Opens in a new window] ,
JIMING MA Open the ORCID record for JIMING MA [Opens in a new window]  and
QIANG ZHANG Open the ORCID record for QIANG ZHANG [Opens in a new window]
JIALIN LEI
Affiliation:
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, PR China e-mail: [email protected]
JIMING MA
Affiliation:
School of Mathematical Sciences, Fudan University, Shanghai 200433, PR China e-mail: [email protected]
QIANG ZHANG*
Affiliation:
School of Mathematics and Statistics, Xi’an Jiaotong University, Xi’an 710049, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate when a group of the form 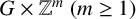$G\times \mathbb {Z}^m\ (m\geq 1)$ has the finitely generated fixed subgroup property of automorphisms (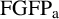$\mathrm {FGFP_a}$), by using the BNS-invariant, and provide some partial answers and nontrivial examples.

Keywords

fixed subgroupBNS-invariantHowson propertyhyperbolic 3-manifolddirect product

MSC classification

Primary: 20F65: Geometric group theory
Secondary: 20F34: Fundamental groups and their automorphisms 57M07: Topological methods in group theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

The authors are partially supported by NSFC (Nos. 12171092, 12271385 and 12471066) and the Shaanxi Fundamental Science Research Project for Mathematics and Physics (Grant No. 23JSY027).

References

Antolín, Y. and Jaikin-Zapirain, A., ‘The Hanna Neumann conjecture for surface groups’, Compos. Math. 158(9) (2022), 1850–1877.CrossRefGoogle Scholar
Bestvina, M. and Handel, M., ‘Train tracks and automorphisms of free groups’, Ann. of Math. (2) 135 (1992), 1–51.CrossRefGoogle Scholar
Bieri, R., Neumann, W. D. and Strebel, R., ‘A geometric invariant of discrete groups’, Invent. Math. 90(3) (1987), 451–477.CrossRefGoogle Scholar
Bieri, R. and Renz, B., ‘Valuations on free resolutions and higher geometric invariants of groups’, Comment. Math. Helv. 63(3) (1988), 464–497.CrossRefGoogle Scholar
Canary, R. D., ‘Covering theorems for hyperbolic 3-manifolds’, in: Conference Proceedings and Lecture Notes in Geometry and Topology, Vol. III (ed. Johannson, K.) (International Press, Cambridge, MA, 1994), 21–30.Google Scholar
Ciobanu, L. and Logan, A., ‘Fixed points and stable images of endomorphisms for the free group of rank two’. J. Algebra 591 (2022), 538–576.CrossRefGoogle Scholar
Dyer, J. and Scott, P., ‘Periodic automorphisms of free groups’, Comm. Algebra 3 (1975), 195–201.CrossRefGoogle Scholar
Friedman, J., Sheaves on Graphs, their Homological Invariants, and a Proof of the Hanna Neumann Conjecture, Memoirs of the American Mathematical Society, 233 (American Mathematical Society, Providence, RI, 2014); with an Appendix by Warren Dicks.Google Scholar
Higman, G., Finitely Presented Infinite Simple Groups, Notes on Pure Mathematics, 8, Department of Mathematics, Institute of Advanced Studies (Australian National University, Canberra, 1974).Google Scholar
Howson, A. G., ‘On the intersection of finitely generated free groups’, J. Lond. Math. Soc. (2) 29 (1954), 428–434.CrossRefGoogle Scholar
Imrich, W. and Turner, E., ‘Endomorphism of free groups and their fixed points’, Math. Proc. Cambridge Philos. Soc. 105 (1989), 421–422.CrossRefGoogle Scholar
Jaikin-Zapirain, A., ‘Free groups are ${L}^2$ -subgroup rigid’, Preprint, 2024, arXiv:2403.09515.Google Scholar
Jiang, B., Wang, S. D. and Zhang, Q., ‘Bounds for fixed points and fixed subgroups on surfaces and graphs’, Algebr. Geom. Topol. 11 (2011), 2297–2318.CrossRefGoogle Scholar
Kochloukova, D., ‘On subdirect products of type $\mbox{FP}_m$ of limit groups’, J. Group Theory 13(1) (2010), 1–19.CrossRefGoogle Scholar
Lei, J. and Zhang, Q., ‘Explicit bounds for fixed subgroups of endomorphisms of free products’, J. Algebra 633 (2023), 773–787.CrossRefGoogle Scholar
Lin, J. and Wang, S., ‘Fixed subgroups of automorphisms of hyperbolic 3-manifold groups’, Topology Appl. 173 (2014), 175–187.CrossRefGoogle Scholar
Meier, J. and Vanwyk, L., ‘The Bieri–Neumann–Strebel invariants for graph groups’, Proc. Lond. Math. Soc. (3) 71 (1995), 263–280.CrossRefGoogle Scholar
Minasyan, A. and Osin, D., ‘Fixed subgroups of automorphisms of relatively hyperbolic groups’, Q. J. Math. 63(3) (2012), 695–712.CrossRefGoogle Scholar
Mineyev, I., ‘Submultiplicativity and the Hanna Neumann conjecture’, Ann. of Math. (2) 175 (2012), 393–414.CrossRefGoogle Scholar
Neumann, W., ‘The fixed group of an automorphism of a word hyperbolic group is rational’, Invent. Math. 110(1) (1992), 147–150.CrossRefGoogle Scholar
Paulin, F., ‘Points fixes des automorphismes de groupe hyperbolique’, Ann. Inst. Fourier (Grenoble) 39(3) (1989), 651–662.CrossRefGoogle Scholar
Rolfsen, D., Knots and Links, Mathematics Lectures Series, 7 (Publish or Perish, Berkeley, CA, 1976).Google Scholar
Roy, M. and Ventura, E., ‘Degrees of compression and inertia for free-abelian times free groups’, J. Algebra 568 (2021), 241–272.CrossRefGoogle Scholar
Shor, J., On Fixed Subgroups of Automorphisms in Hyperbolic Groups, PhD Thesis (Columbia University, 1999).Google Scholar
Soma, T., ‘3-manifold groups with the finitely generated intersection property’, Trans. Amer. Math. Soc. 331(2) (1992), 761–769.Google Scholar
Spahn, R. and Zaremsky, M., ‘The BNSR-invariants of the Stein group ${F}_{2,3}$ ’, J. Group Theory 24(6) (2021), 1149–1162.CrossRefGoogle Scholar
Thurston, W. P., A Norm for the Homology of 3-manifolds, Memoirs of the American Mathematical Society, 59 (American Mathematical Society, Providence, RI, 1986).Google Scholar
Zhang, Q., Ventura, E. and Wu, J., ‘Fixed subgroups are compressed in surface groups’, Internat. J. Algebra Comput. 25 (2015), 865–887.CrossRefGoogle Scholar
Zhang, Q. and Zhao, X., ‘Fixed point indices and fixed words at infinity of selfmaps of graphs’, Topology Appl. 302 (2021), Article no. 107819, 25 pages.CrossRefGoogle Scholar
Zhang, Q. and Zhao, X., ‘Fixed point indices and fixed words at infinity of selfmaps of graphs II’, Topol. Methods Nonlinear Anal. 61(1) (2023), 257–267.Google Scholar
Zhang, Q. and Zhao, X., ‘Aspherical manifolds which do not have Bounded Index Property’, Topology Appl. 341 (2024), Article no. 108757, 8 pages.CrossRefGoogle Scholar