No CrossRef data available.
Published online by Cambridge University Press: 23 April 2018
Let 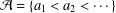 ${\mathcal{A}}=\{a_{1}<a_{2}<\cdots \,\}$ be a set of nonnegative integers. Put
${\mathcal{A}}=\{a_{1}<a_{2}<\cdots \,\}$ be a set of nonnegative integers. Put 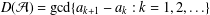 $D({\mathcal{A}})=\gcd \{a_{k+1}-a_{k}:k=1,2,\ldots \}$. The set
$D({\mathcal{A}})=\gcd \{a_{k+1}-a_{k}:k=1,2,\ldots \}$. The set 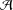 ${\mathcal{A}}$ is an asymptotic basis if there exists
${\mathcal{A}}$ is an asymptotic basis if there exists 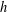 $h$ such that every sufficiently large integer is a sum of at most
$h$ such that every sufficiently large integer is a sum of at most 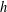 $h$ (not necessarily distinct) elements of
$h$ (not necessarily distinct) elements of 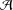 ${\mathcal{A}}$. We prove that if the difference of consecutive integers of
${\mathcal{A}}$. We prove that if the difference of consecutive integers of 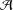 ${\mathcal{A}}$ is bounded, then
${\mathcal{A}}$ is bounded, then 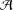 ${\mathcal{A}}$ is an asymptotic basis if and only if there exists an integer
${\mathcal{A}}$ is an asymptotic basis if and only if there exists an integer 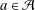 $a\in {\mathcal{A}}$ such that
$a\in {\mathcal{A}}$ such that 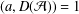 $(a,D({\mathcal{A}}))=1$.
$(a,D({\mathcal{A}}))=1$.
This work was supported by the National Natural Science Foundation of China (Grant No.11471017).