Hostname: page-component-669899f699-8p65j Total loading time: 0 Render date: 2025-04-27T22:35:13.185Z Has data issue: false hasContentIssue false
  • English
  • Français

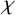A NOTE ON $\chi $-BINDING FUNCTIONS AND LINEAR FORESTS

Part of: Graph theory

Published online by Cambridge University Press:  27 September 2024

KAIYANG LAN Open the ORCID record for KAIYANG LAN [Opens in a new window] ,
FENG LIU Open the ORCID record for FENG LIU [Opens in a new window] ,
DI WU Open the ORCID record for DI WU [Opens in a new window]  and
YIDONG ZHOU Open the ORCID record for YIDONG ZHOU [Opens in a new window]
KAIYANG LAN
Affiliation:
School of Mathematics and Statistics, Minnan Normal University, Zhangzhou Fujian, 363000, PR China e-mail: [email protected]
FENG LIU*
Affiliation:
Department of Mathematics, East China Normal University, Shanghai 200241, PR China
DI WU
Affiliation:
Department of Mathematics and Physics, Nanjing Institute of Technology, Nanjing 211167, Jiangsu, PR China e-mail: [email protected]
YIDONG ZHOU
Affiliation:
College of Computer Science, Nankai University, Tianjin 300350, PR China e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let G and H be two vertex disjoint graphs. The join 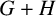$G+H$ is the graph with 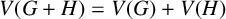$V(G+H)=V(G)+V(H)$ and 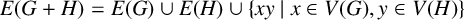$E(G+H)=E(G)\cup E(H)\cup \{xy\;|\; x\in V(G), y\in V(H)\}$. A (finite) linear forest is a graph consisting of (finite) vertex disjoint paths. We prove that for any finite linear forest F and any nonnull graph H, if 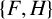$\{F, H\}$-free graphs have a 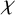$\chi $-binding function 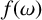$f(\omega )$, then 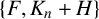$\{F, K_n+H\}$-free graphs have a 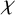$\chi $-binding function 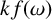$kf(\omega )$ for some constant k.

Keywords

chromatic numberPt-freeinduced subgraph

MSC classification

Primary: 05C15: Coloring of graphs and hypergraphs
Secondary: 05C17: Perfect graphs 05C69: Dominating sets, independent sets, cliques
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This paper was partially supported by grants from the National Natural Sciences Foundation of China (No. 12271170) and Science and Technology Commission of Shanghai Municipality (STCSM) (No. 22DZ2229014).

References

Bondy, J. A. and Murty, U. S. R., Graph Theory (Springer, New York, 2008).CrossRefGoogle Scholar
Briański, M., Davies, J. and Walczak, B., ‘Separating polynomial $\chi$ -boundedness from $\chi$ -boundedness’, Combinatorica 44 (2024), 1–8.CrossRefGoogle Scholar
Char, A. and Karthick, T., ‘Improved bounds on the chromatic number of $\left\{{P}_5,\mathrm{flag}\right\}$ -free graphs’, Discrete Math. 346 (2023), Article no. 113501.CrossRefGoogle Scholar
Chudnovsky, M., Robertson, N., Seymour, P. and Thomas, R., ‘The strong perfect graph theorem’, Ann. of Math. (2) 164 (2006), 51–229.CrossRefGoogle Scholar
Chudnovsky, M., Scott, A. and Seymour, P., ‘Induced subgraphs of graphs with large chromatic number. XII. Distant stars’, J. Graph Theory 92 (2019), 237–254.CrossRefGoogle Scholar
Chudnovsky, M., Scott, A., Seymour, P. and Spirkl, S., ‘Polynomial bounds for chromatic number. VI. Adding a four-vertex path’, European J. Combin. 110 (2023), Article no. 103710.CrossRefGoogle Scholar
Chudnovsky, M., Scott, A., Seymour, P. and Spirkl, S., ‘Polynomial bounds for chromatic number. VII. Disjoint holes’, J. Graph Theory 104 (2023), 499–515.CrossRefGoogle Scholar
Chudnovsky, M. and Sivaraman, V., ‘Perfect divisibility and 2-divisibility’, J. Graph Theory 90 (2019), 54–60.CrossRefGoogle Scholar
Erdős, P., ‘Graph theory and probability’, Canad. J. Math. 11 (1959), 34–38.CrossRefGoogle Scholar
Erdős, P. and Hajnal, A., ‘On spanned subgraphs of graphs’, in: Contributions to Graph Theory and its Applications (Internat. Colloq., Oberhof, 1977) (Tech. Hochschule Ilmenau, Ilmenau, 1977), 80–96 (in German).Google Scholar
Erdős, P. and Hajnal, A., ‘Ramsey-type theorems’, Discrete Appl. Math. 25 (1989), 37–52.CrossRefGoogle Scholar
Esperet, L., Graph Colorings, Flows and Perfect Matchings, Habilitation thesis (Université Grenoble Alpes, 2017). https://tel.archives-ouvertes.fr/tel-01850463/document.Google Scholar
Esperet, L., Lemoine, L., Maffray, F. and Morel, M., ‘The chromatic number of $\left\{{P}_5,{K}_4\right\}$ -free graphs’, Discrete Math. 313 (2013), 743–754.CrossRefGoogle Scholar
Gravier, S., Hoàng, C. T. and Maffray, F., ‘Coloring the hypergraph of maximal cliques of a graph with no long path’, Discrete Math. 272 (2003), 285–290.CrossRefGoogle Scholar
Gyárfás, A., ‘On Ramsey covering-numbers’, Infin. Finite Sets 2 (1975), 801–816.Google Scholar
Gyárfás, A., Szemerédi, E. and Tuza, Z., ‘Induced subtrees in graphs of large chromatic number’, Discrete Math. 30 (1980), 235–344.CrossRefGoogle Scholar
Kierstead, H. A. and Penrice, S. G., ‘Radius two trees specify $\chi$ -bounded classes’, J. Graph Theory 18 (1994), 119–129.CrossRefGoogle Scholar
Kierstead, H. A. and Zhu, Y., ‘Radius three trees in graphs with large chromatic number’, SIAM J. Discrete Math. 17 (2004), 571–581.CrossRefGoogle Scholar
Liu, X., Schroeder, J., Wang, Z. and Yu, X., ‘Polynomial $\chi$ -binding functions for $t$ -broom-free graphs’, J. Combin. Theory Ser. B 162 (2023), 118–133.CrossRefGoogle Scholar
Randerath, B. and Schiermeyer, I., ‘Vertex colouring and forbidden subgraphs: a survey’, Graphs Combin. 20 (2004), 1–40.CrossRefGoogle Scholar
Schiermeyer, I., ‘Chromatic number of ${P}_5$ -free graphs: Reed’s conjecture’, Discrete Math. 339 (2016), 1940–1943.CrossRefGoogle Scholar
Schiermeyer, I. and Randerath, B., ‘Polynomial $\chi$ -binding functions and forbidden induced subgraphs: a survey’, Graphs Combin. 35 (2019), 1–31.CrossRefGoogle Scholar
Scott, A., ‘Induced trees in graphs of large chromatic number’, J. Graph Theory 24 (1997), 297–311.3.0.CO;2-J>CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘A survey of $\chi$ -boundedness’, J. Graph Theory 95 (2020), 473–504.CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘Induced subgraphs of graphs with large chromatic number. XIII. New brooms’, European J. Combin. 84 (2020), Article no. 103024.CrossRefGoogle Scholar
Scott, A. and Seymour, P., ‘Polynomial bounds for chromatic number. V. Excluding a tree of radius two and a complete multipartite graph’, J. Combin. Theory Ser. B 164 (2024), 473–491.CrossRefGoogle Scholar
Scott, A., Seymour, P. and Spirkl, S., ‘Polynomial bounds for chromatic number. II. Excluding a star forest’, J. Graph Theory 101 (2022), 318–322.CrossRefGoogle Scholar
Scott, A., Seymour, P. and Spirkl, S., ‘Polynomial bounds for chromatic number. III. Excluding a double star’, J. Graph Theory 101 (2022), 323–340.CrossRefGoogle Scholar
Scott, A., Seymour, P. and Spirkl, S., ‘Polynomial bounds for chromatic number. I. Excluding a biclique and an induced tree’, J. Graph Theory 102 (2023), 458–471.CrossRefGoogle Scholar
Scott, A., Seymour, P. and Spirkl, S., ‘Polynomial bounds for chromatic number. IV. A near-polynomial bound for excluding the five-vertex path’, Combinatorica 43 (2023), 845–852.CrossRefGoogle Scholar
Seinsche, D., ‘On a property of the class of $n$ -colorable graphs’, J. Combin. Theory Ser. B 16 (1974), 191–193.CrossRefGoogle Scholar
Sumner, D. P., ‘Subtrees of a graph and the chromatic number’, in: The Theory and Applications of Graphs, Kalamazoo, MI, 1980 (ed. Chartrand, G.) (Wiley, New York, 1981), 557–576.Google Scholar
Wagon, S., ‘A bound on the chromatic number of graphs without certain induced subgraphs’, J. Combin. Theory Ser. B 29 (1980), 345–346.CrossRefGoogle Scholar
Wu, D. and Xu, B., ‘Coloring of some crown-free graphs’, Graphs Combin. 39 (2023), Article no. 106.CrossRefGoogle Scholar