Let $[a_1(x),a_2(x),\ldots ,a_n(x),\ldots ]$ be the continued fraction expansion of 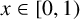$x\in [0,1)$ and 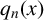$q_n(x)$ be the denominator of its nth convergent. The irrationality exponent and Khintchine exponent of x are respectively defined by

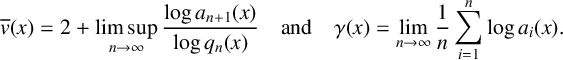$$ \begin{align*} \overline{v}(x)=2+\limsup_{n\to\infty}\frac{\log a_{n+1}(x)}{\log q_n(x)} \quad \text{and}\quad \gamma(x)=\lim_{n\to\infty}\frac{1}{n}\sum_{i=1}^{n}\log a_i(x). \end{align*} $$

We study the multifractal spectrum of the irrationality exponent and the Khintchine exponent for continued fractions with nondecreasing partial quotients. For any 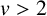$v>2$, we completely determine the Hausdorff dimensions of the sets 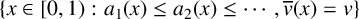$\{x\in [0,1): a_1(x)\leq a_2(x)\leq \cdots , \overline {v}(x)=v\}$ and

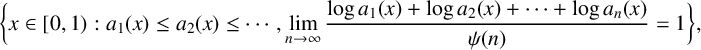$$ \begin{align*}\bigg\{x\in[0,1): a_1(x)\leq a_2(x)\leq\cdots, \lim\limits_{n\to\infty}\frac{\log a_1(x)+\log a_2(x)+\cdots+\log a_n(x)}{\psi(n)}=1\bigg\},\end{align*} $$

where 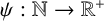$\psi :\mathbb {N}\rightarrow \mathbb {R}^+$ is a function satisfying 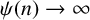$\psi (n)\to \infty $ as 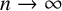$n\to \infty $.