Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-04T22:30:56.980Z Has data issue: false hasContentIssue false
  • English
  • Français

MONOGENIC QUARTIC POLYNOMIALS AND THEIR GALOIS GROUPS

Part of: Algebraic number theory: global fields

Published online by Cambridge University Press:  11 October 2024

JOSHUA HARRINGTON Open the ORCID record for JOSHUA HARRINGTON [Opens in a new window]  and
LENNY JONES Open the ORCID record for LENNY JONES [Opens in a new window]
JOSHUA HARRINGTON
Affiliation:
Department of Mathematics, Cedar Crest College, Allentown, Pennsylvania, USA e-mail: [email protected]
LENNY JONES*
Affiliation:
Department of Mathematics, Shippensburg University, Shippensburg, Pennsylvania, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

A monic polynomial 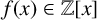$f(x)\in {\mathbb Z}[x]$ of degree N is called monogenic if 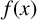$f(x)$ is irreducible over 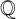${\mathbb Q}$ and 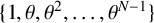$\{1,\theta ,\theta ^2,\ldots ,\theta ^{N-1}\}$ is a basis for the ring of integers of 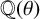${\mathbb Q}(\theta )$, where 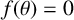$f(\theta )=0$. We use the classification of the Galois groups of quartic polynomials, due to Kappe and Warren [‘An elementary test for the Galois group of a quartic polynomial’, Amer. Math. Monthly 96(2) (1989), 133–137], to investigate the existence of infinite collections of monogenic quartic polynomials having a prescribed Galois group, such that each member of the collection generates a distinct quartic field. With the exception of the cyclic case, we provide such an infinite single-parameter collection for each possible Galois group. We believe these examples are new and we provide evidence to support this belief by showing that they are distinct from other infinite collections in the literature. Finally, we devote a separate section to the cyclic case.

Keywords

monogenicquartic polynomialGalois group

MSC classification

Primary: 11R16: Cubic and quartic extensions
Secondary: 11R32: Galois theory
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 244 - 259
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Booker, A. R. and Browning, T. D., ‘Square-free values of reducible polynomials’, Discrete Anal. 2016 (2016), Article no. 8, 16 pages.Google Scholar
Chang, M.-L., ‘Monogeneity in biquadratic fields’, Int. J. Pure Appl. Math. 31(4) (2006), 481–490.Google Scholar
Cohen, H., A Course in Computational Algebraic Number Theory, Graduate Texts in Mathematics, 138 (Springer-Verlag, Berlin–Heidelberg, 2000).Google Scholar
Gaál, I., ‘Calculating power integral bases in some quartic fields corresponding to monogenic families of polynomials’, Preprint, 2024, arXiv:2405.13429v1.CrossRefGoogle Scholar
Gassert, T., Smith, H. and Stange, K., ‘A family of monogenic ${S}_4$ quartic fields arising from elliptic curves’, J. Number Theory 197 (2019), 361–382.CrossRefGoogle Scholar
Gras, M.-N., ‘ $\mathbb{Z}$ -bases d’entiers 1, $\theta$ , ${\theta}^2$ , ${\theta}^3$ dans les extensions cycliques de degré 4 de $\mathbb{Q}$ ’, in: Number Theory, 1979–1980 and 1980–1981 (Publications Mathématiques de la Faculté des Sciences de Besançon, Université de Franche-Comté, Besançon, 1981), exp. no. 6, 14 pages.Google Scholar
Gras, M.-N. and Tanoé, F., ‘Corps biquadratiques monogènes’, Manuscripta Math. 86(1) (1995), 63–79.CrossRefGoogle Scholar
Huard, J., Spearman, B. and Williams, K., ‘Integral bases for quartic fields with quadratic subfields’, J. Number Theory 51(1) (1995), 87–102.CrossRefGoogle Scholar
Jones, L., ‘Infinite families of reciprocal monogenic polynomials and their Galois groups’, New York J. Math. 27 (2021), 1465–1493.Google Scholar
Kable, A., ‘Power bases in dihedral quartic fields’, J. Number Theory 76(1) (1999), 120–129.CrossRefGoogle Scholar
Kappe, L.-C. and Warren, B., ‘An elementary test for the Galois group of a quartic polynomial’, Amer. Math. Monthly 96(2) (1989), 133–137.CrossRefGoogle Scholar
Ledermann, W. and van der Ploeg, C., ‘Integral bases of dihedral number fields I’, J. Aust. Math. Soc. Ser. A 38(3) (1985), 351–371.CrossRefGoogle Scholar
Motoda, Y., Nakahara, T., Shah, A. S. I. and Uehara, T., ‘On a problem of Hasse’, in: Algebraic Number Theory and Related Topics 2007, RIMS Kôkyûroku Bessatsu, B12 (eds. Asada, M., Nakamura, H. and Takahashi, H.) (Research Institute for Mathematical Sciences (RIMS), Kyoto, 2009), 209–221.Google Scholar
Nyul, G., ‘Power integral bases in mixed biquadratic number fields’, Acta Acad. Paedagog. Agriensis Sect. Math. (N.S.) 28 (2001), 79–86.Google Scholar
Olajos, P., ‘Power integral bases in the family of simplest quartic fields’, Exp. Math. 14(2) (2005), 129–132.CrossRefGoogle Scholar
Perron, O., ‘Neue Kriterien für die Irreduzibilität algebraischer Gleichungen’, J. reine angew. Math. 132 (1907), 288–307.Google Scholar
Smith, H., ‘Two families of monogenic ${S}_4$ quartic number fields’, Acta Arith. 186(3) (2018), 257–271.CrossRefGoogle Scholar
Spearman, B., ‘Monogenic ${A}_4$ quartic fields’, Int. Math. Forum 1(37–40) (2006), 1969–1974.CrossRefGoogle Scholar
Voutier, P., ‘A family of cyclic quartic monogenic polynomials’, Preprint, 2024, arXiv:2405.20288v1.Google Scholar
Williams, K., ‘Integers of biquadratic fields’, Canad. Math. Bull. 13 (1970), 519–526.CrossRefGoogle Scholar