Hostname: page-component-669899f699-swprf Total loading time: 0 Render date: 2025-05-02T07:15:45.012Z Has data issue: false hasContentIssue false
  • English
  • Français

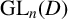LOCALLY NILPOTENT SUBGROUPS OF $\mathrm {GL}_n(D)$

Part of: Other groups of matrices Basic linear algebra Division rings and semisimple Artin rings

Published online by Cambridge University Press:  06 November 2024

R. FALLAH-MOGHADDAM Open the ORCID record for R. FALLAH-MOGHADDAM [Opens in a new window]  and
H. R. DORBIDI Open the ORCID record for H. R. DORBIDI [Opens in a new window]
R. FALLAH-MOGHADDAM*
Affiliation:
Department of Mathematics Education, Farhangian University, P.O. Box 14665-889, Tehran, Iran
H. R. DORBIDI
Affiliation:
Department of Mathematics, Faculty of Science, University of Jiroft, Jiroft 78671-61167, Iran e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Let A be an F-central simple algebra of degree 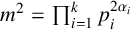$m^2=\prod _{i=1}^k p_i^{2\alpha _i}$ and G be a subgroup of the unit group of A such that 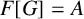$F[G]=A$. We prove that if G is a central product of two of its subgroups M and N, then 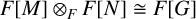$F[M]\otimes _F F[N]\cong F[G]$. Also, if G is locally nilpotent, then G is a central product of subgroups 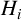$H_i$, where 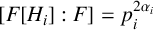$[F[H_i]:F]=p_i^{2\alpha _i}$, 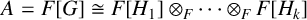$A=F[G]\cong F[H_1]\otimes _F \cdots \otimes _F F[H_k]$ and 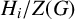$H_i/Z(G)$ is the Sylow 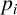$p_i$-subgroup of 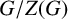$G/Z(G)$ for each i with 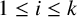$1\leq i\leq k$. Additionally, there is an element of order 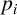$p_i$ in F for each i with 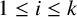$1\leq i\leq k$.

Keywords

division ringlocally nilpotent subgroupcentral product of groupscrossed product

MSC classification

Primary: 16K20: Finite-dimensional
Secondary: 15A30: Algebraic systems of matrices 20H25: Other matrix groups over rings
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 11
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Akbari, S., Ebrahimian, R., Momenaee Kermani, H. and Salehi Golsefidy, A., ‘Maximal subgroups of ${GL}_n(D)$ ’, J. Algebra 259 (2003), 201–225.CrossRefGoogle Scholar
Akbari, S., Mahdavi-Hezavehi, M. and Mahmudi, M. G., ‘Maximal subgroups of ${GL}_1(D)$ ’, J. Algebra 217 (1999), 422–433.CrossRefGoogle Scholar
Amitsur, S. A., ‘Finite subgroups of division rings’, Trans. Amer. Math. Soc. 80 (1955), 361–386.CrossRefGoogle Scholar
Dixon, J. D., The Structure of Linear Groups, Van Nostrand Reinhold Mathematical Studies, 37 (John Wiley and Sons, Hoboken, NJ, 1971).Google Scholar
Dorbidi, H., Fallah-Moghaddam, R. and Mahdavi-Hezavehi, M., ‘Soluble maximal subgroups of ${GL}_n(D)$ ’, J. Algebra Appl. 9(6) (2010), 921–932.Google Scholar
Draxl, P. K., Skew Fields (Cambridge University Press, Cambridge, 1983).CrossRefGoogle Scholar
Ebrahimian, R., ‘Nilpotent maximal subgroups of ${GL}_n(D)$ ’, J. Algebra 280 (2004), 244–248.CrossRefGoogle Scholar
Ebrahimian, R., Kiani, D. and Mahdavi-Hezavehi, M., ‘Supersoluble crossed product criterion for division algebras’, Israel J. Math. 145 (2005), 325–331.CrossRefGoogle Scholar
Fallah-Moghaddam, R., ‘Maximal subgroups of ${SL}_n(D)$ ’, J. Algebra 531 (2019), 70–82.CrossRefGoogle Scholar
Garascuk, M. S., ‘On the theory of the generalized nilpotent linear groups’, Dokl. Akad. Nauk BSSR 4 (1960), 276–277.Google Scholar
Hazrat, R., Mahdavi-Hezavehi, M. and Motiee, M., ‘Multiplicative groups of division rings’, Math. Proc. R. Ir. Acad. 114(1) (2014), 37–114.CrossRefGoogle Scholar
Hazrat, R. and Wadsworth, A. R., ‘On maximal subgroups of the multiplicative group of a division algebra’, J. Algebra 322 (2009), 2528–2543.CrossRefGoogle Scholar
Herstein, I. N., ‘Finite multiplicative subgroups in division rings’, Pacific J. Math. 3 (1953), 121–126.CrossRefGoogle Scholar
Herstein, I. N., ‘Multiplicative commutators in division rings’, Israel J. Math. 31(2) (1978), 180–188.CrossRefGoogle Scholar
Hua, L. K., ‘Some properties of a field’, Proc. Natl. Acad. Sci. USA 35 (1949), 533–537.CrossRefGoogle Scholar
Hua, L. K., ‘On the multiplicative group of a field’, Sci. Rec. Acad. Sin. 3 (1950), 1–6.Google Scholar
Huzurbazar, M. S., ‘The multiplicative group of a division ring’, Dokl. Akad. Nauk SSSR 131 (1960), 1268–1271; English translation Soviet Math. Dokl. 1 (1960), 433–435.Google Scholar
Keshavarzipour, T. and Mahdavi-Hezavehi, M., ‘Crossed product conditions for central simple algebras in terms of irreducible subgroups’, J. Algebra 315(2) (2007), 738–744.CrossRefGoogle Scholar
Kiani, D. and Ramezan-Nassab, M., ‘Crossed product conditions for central simple algebras in terms of splitting fields’, Int. Math. Forum 4(32) (2009), 1587–1590.Google Scholar
Mahdavi-Hezavehi, M. and Tignol, J.-P., ‘Cyclicity conditions for division algebras of prime degree’, Proc. Amer. Math. Soc. 131(12) (2003), 3673–3676.CrossRefGoogle Scholar
Pierce, R. S., Associative Algebras, Graduate Texts in Mathematics, 88 (Springer, New York, 1986).Google Scholar
Robinson, D. J. S., A Course in the Theory Groups, Graduate Texts in Mathematics, 80 (Springer, New York, 1982).CrossRefGoogle Scholar
Scott, W. R., ‘On the multiplicative group of a division ring’, Proc. Amer. Math. Soc. 8 (1957), 303–305.CrossRefGoogle Scholar
Scott, W. R., Group Theory (Dover, New York, 1987).Google Scholar
Shirvani, M. and Wehrfritz, B. A. F., Skew Linear Groups, London Mathematical Society Lecture Note Series, 118 (Cambridge University Press, Cambridge, 1986).Google Scholar
Suprunenko, D. A., Matrix Groups (American Mathematical Society, Providence, RI, 1976).CrossRefGoogle Scholar
Wehrfritz, B. A. F., Infinite Linear Groups, Ergebnisse der Mathematik und ihrer Grenzgebiete, 76 (Springer-Verlag, Berlin–Heidelberg–New York, 1973).CrossRefGoogle Scholar
Wehrfritz, B. A. F., ‘Locally nilpotent skew linear groups’, Proc. Edinb. Math. Soc. (2) 29 (1986), 101–113.CrossRefGoogle Scholar
Wehrfritz, B. A. F., ‘Locally nilpotent skew linear groups II’, Proc. Edinb. Math. Soc. (2) 30 (1987), 423–426.CrossRefGoogle Scholar
Zaleeskii, A. E., ‘The structure of several classes of matrix groups over a division ring’, Sibirsk. Mat. Zh. 8 (1967), 1284–1298 (in Russian).Google Scholar