Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-27T13:48:21.421Z Has data issue: false hasContentIssue false
  • English
  • Français

LINEAR SYSTEMS OF GEOMETRICALLY IRREDUCIBLE PLANE CUBICS OVER FINITE FIELDS

Part of: Curves Arithmetic problems. Diophantine geometry Cycles and subschemes Projective and enumerative geometry

Published online by Cambridge University Press:  27 February 2025

SHAMIL ASGARLI Open the ORCID record for SHAMIL ASGARLI [Opens in a new window]  and
DRAGOS GHIOCA Open the ORCID record for DRAGOS GHIOCA [Opens in a new window]
SHAMIL ASGARLI
Affiliation:
Department of Mathematics and Computer Science, Santa Clara University, 500 El Camino Real, CA 95053, USA e-mail: [email protected]
DRAGOS GHIOCA*
Affiliation:
Department of Mathematics, University of British Columbia, Vancouver, BC V6T 1Z2, Canada
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We examine the maximum dimension of a linear system of plane cubic curves whose 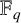$\mathbb {F}_q$-members are all geometrically irreducible. Computational evidence suggests that such a system has a maximum (projective) dimension of 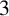$3$. As a step towards the conjecture, we prove that there exists a three-dimensional linear system 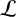$\mathcal {L}$ with at most one geometrically reducible $\mathbb {F}_q$-member.

Keywords

linear systemcubic curvegeometric irreducibilityfinite field

MSC classification

Primary: 14N05: Projective techniques
Secondary: 14C21: Pencils, nets, webs 14H50: Plane and space curves 14G15: Finite ground fields
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 9
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Asgarli, S., Ghioca, D. and Reichstein, Z., ‘Linear families of smooth hypersurfaces over finitely generated fields’, Finite Fields Appl. 87 (2023), Article no. 102169, 10 pages.CrossRefGoogle Scholar
Asgarli, S., Ghioca, D. and Reichstein, Z., ‘Linear system of hypersurfaces passing through a Galois orbit’, Res. Number Theory 10(4) (2024), Article no. 84, 16 pages.CrossRefGoogle Scholar
Asgarli, S., Ghioca, D. and Yip, C. H., ‘Existence of pencils with nonblocking hypersurfaces’, Finite Fields Appl. 92 (2023), Article no. 102283, 11 pages.CrossRefGoogle Scholar
Lorenzini, D., ‘Reducibility of polynomials in two variables’, J. Algebra 156(1) (1993), 65–75.CrossRefGoogle Scholar
Pereira, J. V. and Yuzvinsky, S., ‘Completely reducible hypersurfaces in a pencil’, Adv. Math. 219(2) (2008), 672–688.CrossRefGoogle Scholar
The Sage Developers, SageMath, the Sage Mathematics Software System (Version 9.4) (2021). Available at https://www.sagemath.org.Google Scholar
Vistoli, A., ‘The number of reducible hypersurfaces in a pencil’, Invent. Math. 112(2) (1993), 247–262.CrossRefGoogle Scholar