Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-28T19:12:12.907Z Has data issue: false hasContentIssue false
  • English
  • Français

IRREDUCIBLE FAMILIES OF COMPLEX MATRICES CONTAINING A RANK-ONE MATRIX

Part of: Basic linear algebra

Published online by Cambridge University Press:  16 January 2020

W. E. LONGSTAFF Open the ORCID record for W. E. LONGSTAFF [Opens in a new window]
W. E. LONGSTAFF*
Affiliation:
11 Tussock Crescent, Elanora, Queensland4221, Australia email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that an irreducible family 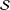${\mathcal{S}}$ of complex 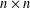$n\times n$ matrices satisfies Paz’s conjecture if it contains a rank-one matrix. We next investigate properties of families of rank-one matrices. If 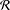${\mathcal{R}}$ is a linearly independent, irreducible family of rank-one matrices then (i) 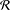${\mathcal{R}}$ has length at most $n$, (ii) if all pairwise products are nonzero, 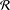${\mathcal{R}}$ has length 1 or 2, (iii) if 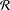${\mathcal{R}}$ consists of elementary matrices, its minimum spanning length 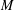$M$ is the smallest integer 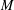$M$ such that every elementary matrix belongs to the set of words in 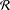${\mathcal{R}}$ of length at most 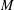$M$. Finally, for any integer 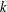$k$ dividing 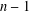$n-1$, there is an irreducible family of elementary matrices with length 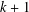$k+1$.

Keywords

irreduciblerank oneelementary matrices

MSC classification

Primary: 15A30: Algebraic systems of matrices
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 102 , Issue 2 , October 2020 , pp. 226 - 236
Check for updates
Copyright
© 2020 Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Guterman, A. E., Laffey, T., Markova, O. V. and Smigoc, H., ‘A resolution of Paz’s conjecture in the presence of a nonderogatory matrix’, Linear Algebra Appl. 543 (2018), 234–250.CrossRefGoogle Scholar
Guterman, A. E., Markova, O. V. and Mehrmann, V., ‘Length realizability for pairs of quasi-commuting matrices’, Linear Algebra Appl. 568 (2019), 135–154.CrossRefGoogle Scholar
Lambrou, M. S. and Longstaff, W. E., ‘On the lengths of pairs of complex matrices of size six’, Bull. Aust. Math. Soc. 80 (2009), 177–201.CrossRefGoogle Scholar
Lomonosov, V. and Rosenthal, P., ‘The simplest proof of Burnside’s theorem on matrix algebras’, Linear Algebra Appl. 383 (2004), 45–47.CrossRefGoogle Scholar
Longstaff, W. E., ‘Burnside’s theorem: irreducible pairs of transformations’, Linear Algebra Appl. 382 (2004), 247–269.CrossRefGoogle Scholar
Longstaff, W. E., ‘On minimal sets of 0, 1-matrices whose pairwise products form a basis for M n(𝔽)’, Bull. Aust. Math. Soc. 98(3) (2018), 402–413.CrossRefGoogle Scholar
Longstaff, W. E., Niemeyer, A. C. and Panaia, O., ‘On the lengths of pairs of complex matrices of size at most five’, Bull. Aust. Math. Soc. 73 (2006), 461–472.CrossRefGoogle Scholar
Longstaff, W. E. and Rosenthal, P., ‘On the lengths of irreducible pairs of complex matrices’, Proc. Amer. Math. Soc. 139(11) (2011), 3769–3777.CrossRefGoogle Scholar
Markova, O. V., ‘Length computation of matrix subalgebras of special type’, Fundam. Prikl. Mat. 13(4) (2007), 165–197; English transl. in: J. Math. Sci. (N. Y.) 155(6) (2008), 908–931.Google Scholar
Markova, O. V., ‘The length function and matrix algebras’, Fundam. Prikl. Mat. 17(6) (2012), 65–173; English transl. in: J. Math. Sci. (N. Y.) 193(5) (2013), 687–768.Google Scholar
Pappacena, C. J., ‘An upper bound for the length of a finite-dimensional algebra’, J. Algebra 197 (1997), 535–545.CrossRefGoogle Scholar
Paz, A., ‘An application of the Cayley–Hamilton theorem to matrix polynomials in several variables’, Linear Multilinear Algebra 15 (1984), 161–170.CrossRefGoogle Scholar
Radjavi, H. and Rosenthal, P., Simultaneous Triangularization (Springer, New York, 2000).CrossRefGoogle Scholar
Shitov, Y., ‘An improved bound for the lengths of matrix algebras’, Algebra Number Theory 13(6) (2019), 1501–1507; (English summary).CrossRefGoogle Scholar