Hostname: page-component-669899f699-tpknm Total loading time: 0 Render date: 2025-04-30T22:49:38.204Z Has data issue: false hasContentIssue false
  • English
  • Français

HOMOLOGICAL LINEAR QUOTIENTS AND EDGE IDEALS OF GRAPHS

Part of: General commutative ring theory Commutative algebra: Homological methods Graph theory Arithmetic rings and other special rings

Published online by Cambridge University Press:  29 January 2024

NADIA TAGHIPOUR Open the ORCID record for NADIA TAGHIPOUR [Opens in a new window] ,
SHAMILA BAYATI Open the ORCID record for SHAMILA BAYATI [Opens in a new window]  and
FARHAD RAHMATI Open the ORCID record for FARHAD RAHMATI [Opens in a new window]
NADIA TAGHIPOUR
Affiliation:
Department of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran e-mail: [email protected]
SHAMILA BAYATI*
Affiliation:
Department of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran
FARHAD RAHMATI
Affiliation:
Department of Mathematics and Computer Science, Amirkabir University of Technology (Tehran Polytechnic), Tehran, Iran e-mail: [email protected]
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that the edge ideal 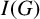$I(G)$ of a simple graph G has linear quotients if and only if 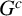$G^c$ is chordal. We investigate when the property of having linear quotients is inherited by homological shift ideals of an edge ideal. We will see that adding a cluster to the graph 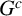$G^c$ when 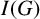$I(G)$ has homological linear quotients results in a graph with the same property. In particular, 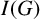$I(G)$ has homological linear quotients when 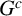$G^c$ is a block graph. We also show that adding pinnacles to trees preserves the property of having homological linear quotients for the edge ideal of their complements. Furthermore, 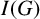$I(G)$ has homological linear quotients for every graph G such that 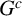$G^c$ is a 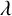$\lambda $-minimal chordal graph.

Keywords

block graphschordal graphsedge idealshomological shift idealsλ-minimal graphslinear quotientsmultigraded shifts

MSC classification

Primary: 13D02: Syzygies, resolutions, complexes
Secondary: 05C25: Graphs and abstract algebra (groups, rings, fields, etc.) 13A02: Graded rings 13F20: Polynomial rings and ideals; rings of integer-valued polynomials
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 110 , Issue 2 , October 2024 , pp. 291 - 302
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Bayati, S., ‘Multigraded shifts of matroidal ideals’, Arch. Math. (Basel) 111(3) (2018), 239–246.10.1007/s00013-018-1216-7CrossRefGoogle Scholar
Bayati, S., ‘A quasi-additive property of homological shift ideals’, Bull. Malays. Math. Sci. Soc. 46(3) (2023), Article no. 111.10.1007/s40840-023-01506-1CrossRefGoogle Scholar
Bayati, S., Jahani, I. and Taghipour, N., ‘Linear quotients and multigraded shifts of Borel ideals’, Bull. Aust. Math. Soc. 100(1) (2019), 48–57.10.1017/S0004972718001600CrossRefGoogle Scholar
Crupi, M. and Ficarra, A., ‘Very well-covered graphs by Betti splittings’, J. Algebra 629 (2023), 76–108.10.1016/j.jalgebra.2023.03.033CrossRefGoogle Scholar
Dirac, G. A., ‘On rigid circuit graphs’, Abh. Math. Semin. Univ. Hambg. 25 (1961), 71–76.10.1007/BF02992776CrossRefGoogle Scholar
Ficarra, A., ‘Homological shifts of polymatroidal ideals’, Preprint, 2022, arXiv:2205.04163v2.Google Scholar
Ficarra, A. and Herzog, J., ‘Dirac’s theorem and multigraded syzygies’, Mediterr. J. Math. 20(3) (2023), Article no. 134.10.1007/s00009-023-02348-8CrossRefGoogle Scholar
Francisco, C., Há, H. T. and Van Tuyl, A., ‘Splittings of monomial ideals’, Proc. Amer. Math. Soc. 137(10) (2009), 3271–3282.10.1090/S0002-9939-09-09929-8CrossRefGoogle Scholar
Frank, O., Harary, F. and Plantholt, M., ‘The line-distinguishing chromatic number of a graph’, Ars Combin. 14 (1982), 241–252.Google Scholar
Fröberg, R., ‘On Stanley–Reisner rings’, in: Topics in Algebra, Banach Center Publications, 26(2) (eds. Balcerzyk, S., Józefiak, T., Krempa, J., Simson, D. and Vogel, W.) (PWN, Warsaw, 1990), 57–70.Google Scholar
Fulkerson, D. R. and Gross, O. A., ‘Incidence matrices and interval graphs’, Pacific J. Math. 15 (1965), 835–855.10.2140/pjm.1965.15.835CrossRefGoogle Scholar
Herzog, J. and Hibi, T., Monomial Ideals (Springer, London, 2011).10.1007/978-0-85729-106-6CrossRefGoogle Scholar
Herzog, J., Moradi, S., Rahimbeigi, M. and Zhu, G., ‘Homological shift ideals’, Collect. Math. 72 (2021), 157–174.10.1007/s13348-020-00284-4CrossRefGoogle Scholar
Herzog, J., Moradi, S., Rahimbeigi, M. and Zhu, G., ‘Some homological properties of Borel type ideals’, Comm. Algebra 51(4) (2023), 1517–1531.10.1080/00927872.2022.2137521CrossRefGoogle Scholar
Herzog, J. and Takayama, Y., ‘Resolutions by mapping cones’, Homology Homotopy Appl. 4(2) (2002), 277–294.10.4310/HHA.2002.v4.n2.a13CrossRefGoogle Scholar
Regonati, F. and Salvi, N. Z., ‘Some constructions of $\lambda$ -minimal graphs’, Czechoslovak Math. J. 44(2) (1994), 315–323.10.21136/CMJ.1994.128459CrossRefGoogle Scholar