Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-29T22:31:53.677Z Has data issue: false hasContentIssue false
  • English
  • Français

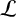GRADIENT ESTIMATES FOR POSITIVE EIGENFUNCTIONS OF THE $\mathcal {L}$-OPERATOR ON CONFORMAL SOLITONS AND THEIR APPLICATIONS

Part of: Global differential geometry Partial differential equations

Published online by Cambridge University Press:  18 November 2024

GUANGWEN ZHAO Open the ORCID record for GUANGWEN ZHAO [Opens in a new window]
GUANGWEN ZHAO*
Affiliation:
Department of Mathematics, School of Sciences, Wuhan University of Technology, Wuhan 430070, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove a local gradient estimate for positive eigenfunctions of the 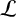$\mathcal {L}$-operator on conformal solitons given by a general conformal vector field. As an application, we obtain a Liouville type theorem for 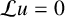$\mathcal {L} u=0$, which improves the one of Li and Sun [‘Gradient estimate for the positive solutions of 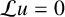$\mathcal Lu = 0$ and 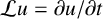$\mathcal Lu ={\partial u}/{\partial t}$ on conformal solitons’, Acta Math. Sin. (Engl. Ser.) 37(11) (2021), 1768–1782]. We also consider applications where manifolds are special conformal solitons and obtain a better Liouville type theorem in the case of self-shrinkers.

Keywords

conformal solitongradient estimateLiouville type theorem

MSC classification

Primary: 53C40: Global submanifolds
Secondary: 35B45: A priori estimates
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 111 , Issue 2 , April 2025 , pp. 344 - 355
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work is partially supported by the National Natural Science Foundation of China (Grant No. 12001410).

References

Arezzo, C. and Sun, J., ‘Conformal solitons to the mean curvature flow and minimal submanifolds’, Math. Nachr. 286(8–9) (2013), 772–790.CrossRefGoogle Scholar
Calabi, E., ‘An extension of E. Hopf’s maximum principle with an application to Riemannian geometry’, Duke Math. J. 25 (1958), 45–56.CrossRefGoogle Scholar
Chen, Q., Jost, J. and Qiu, H., ‘Existence and Liouville theorems for $V$ -harmonic maps from complete manifolds’, Ann. Global Anal. Geom. 42(4) (2012), 565–584.CrossRefGoogle Scholar
Chen, Q., Jost, J. and Wang, G., ‘A maximum principle for generalizations of harmonic maps in Hermitian, affine, Weyl, and Finsler geometry’, J. Geom. Anal. 25(4) (2015), 2407–2426.CrossRefGoogle Scholar
Li, X. and Sun, J., ‘Gradient estimate for the positive solutions of $u=0$ and $u=\frac{\partial u}{\partial t}$ on conformal solitons’, Acta Math. Sin. (Engl. Ser.) 37(11) (2021), 1768–1782.CrossRefGoogle Scholar
Schoen, R. M. and Yau, S.-T., Lectures on Differential Geometry (International Press, Somerville, MA, 1994).Google Scholar
Smoczyk, K., ‘A relation between mean curvature flow solitons and minimal submanifolds’, Math. Nachr. 229 (2001), 175–186.3.0.CO;2-H>CrossRefGoogle Scholar
Wei, G. and Wylie, W., ‘Comparison geometry for the Bakry–Emery Ricci tensor’, J. Differential Geom. 83(2) (2009), 377–405.CrossRefGoogle Scholar
Yau, S. T., ‘Harmonic functions on complete Riemannian manifolds’, Comm. Pure Appl. Math. 28 (1975), 201–228.CrossRefGoogle Scholar
Zhu, Y. and Chen, Q., ‘Gradient estimates for the positive solutions of $u=0$ on self-shrinkers’, Mediterr. J. Math. 15(1) (2018), Article no. 28, 14 pages.CrossRefGoogle Scholar