Hostname: page-component-669899f699-tzmfd Total loading time: 0 Render date: 2025-05-05T18:19:05.879Z Has data issue: false hasContentIssue false
  • English
  • Français

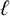EXTENDING CONGRUENCES FOR OVERPARTITIONS WITH $\ell $-REGULAR NONOVERLINED PARTS

Part of: Combinatorics Additive number theory; partitions

Published online by Cambridge University Press:  25 November 2024

JAMES A. SELLERS Open the ORCID record for JAMES A. SELLERS [Opens in a new window]
JAMES A. SELLERS*
Affiliation:
Department of Mathematics and Statistics, University of Minnesota Duluth, Duluth, MN 55812, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Recently, Alanazi et al. [‘Refining overpartitions by properties of nonoverlined parts’, Contrib. Discrete Math. 17(2) (2022), 96–111] considered overpartitions wherein the nonoverlined parts must be 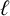$\ell $-regular, that is, the nonoverlined parts cannot be divisible by the integer 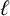$\ell $. In the process, they proved a general parity result for the corresponding enumerating functions. They also proved some specific congruences for the case 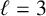$\ell =3$. In this paper we use elementary generating function manipulations to significantly extend this set of known congruences for these functions.

Keywords

partitionscongruencesoverpartitionsgenerating functions

MSC classification

Primary: 11P83: Partitions; congruences and congruential restrictions
Secondary: 05A17: Partitions of integers
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 12
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Alanazi, A. M., Alenazi, B. M., Keith, W. J. and Munagi, A. O., ‘Refining overpartitions by properties of nonoverlined parts’, Contrib. Discrete Math. 17(2) (2022), 96–111.CrossRefGoogle Scholar
Alanazi, A. M., Munagi, A. O. and Sellers, J. A., ‘An infinite family of congruences for $l$ -regular overpartitions’, Integers 16 (2016), Article no. A37.Google Scholar
Andrews, G. E., The Theory of Partitions, Encyclopedia of Mathematics and its Applications, 2 (Addison–Wesley Publishing Co., Reading, MA, 1976).Google Scholar
Andrews, G. E. and Eriksson, K., Integer Partitions (Cambridge University Press, Cambridge, 2004).CrossRefGoogle Scholar
Bharadwaj, H. S. S., Hemanthkumar, B. and Naika, M. S. M., ‘On 3- and 9-regular over partitions modulo powers of 3’, Colloq. Math. 154(1) (2018), 121–130.CrossRefGoogle Scholar
Bringmann, K., Dousse, J., Lovejoy, J. and Mahlburg, K., ‘Overpartitions with restricted odd differences’, Electron. J. Combin. 22(3) (2015), Article no. 3.17.CrossRefGoogle Scholar
Chen, W. Y. C., Hou, Q.-H., Sun, L. H. and Zhang, L., ‘Ramanujan-type congruences for overpartitions modulo 16’, Ramanujan J. 40(2) (2016), 311–322.CrossRefGoogle Scholar
Chen, W. Y. C., Sun, L. H., Wang, R.-H. and Zhang, L., ‘Ramanujan-type congruences for overpartitions modulo 5’, J. Number Theory 148 (2015), 62–72.CrossRefGoogle Scholar
Chen, W. Y. C. and Xia, E. X. W., ‘Proof of a conjecture of Hirschhorn and Sellers on overpartitions’, Acta Arith. 163(1) (2014), 59–69.CrossRefGoogle Scholar
Chetry, J. and Saikia, N., ‘New infinite families of congruences modulo 3, 5 and 7 for overpartition function’, J. Ramanujan Math. Soc. 34(4) (2019), 417–426.Google Scholar
Corteel, S. and Lovejoy, J., ‘Overpartitions’, Trans. Amer. Math. Soc. 356(4) (2004), 1623–1635.CrossRefGoogle Scholar
da Silva, R. and Sellers, J. A., ‘Infinitely many congruences for $k$ -regular partitions with designated summands’, Bull. Braz. Math. Soc. (N.S.) 51(2) (2020), 357–370.CrossRefGoogle Scholar
Dou, D. Q. J. and Lin, B. L. S., ‘New Ramanujan type congruences modulo 5 for overpartitions’, Ramanujan J. 44(2) (2017), 401–410.CrossRefGoogle Scholar
Hirschhorn, M. D., The Power of $q$ : A Personal Journey (Springer, Cham, 2017).Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic properties for overpartitions’, J. Combin. Math. Combin. Comput. 53 (2005), 65–73.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Arithmetic properties of overpartitions into odd parts’, Ann. Comb. 10(3) (2006), 353–367.CrossRefGoogle Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘A congruence modulo 3 for partitions into distinct non-multiples of four’, J. Integer Seq. 17 (2014), Article no. 14.9.6.Google Scholar
Hirschhorn, M. D. and Sellers, J. A., ‘Congruences for overpartitions with restricted odd differences’, Ramanujan J. 53(1) (2020), 167–180.CrossRefGoogle Scholar
Jindal, A. and Meher, N. K., ‘New congruences for $\ell$ -regular overpartitions’, J. Korean Math. Soc. 59(5) (2022), 945–962.Google Scholar
Kim, B., ‘The overpartition function modulo 128’, Integers 8 (2008), Article no. A38.Google Scholar
Lin, B. L. S., Liu, J., Wang, A. Y. Z. and Xiao, J., ‘Infinite families of congruences for overpartitions with restricted odd differences’, Bull. Aust. Math. Soc. 102(1) (2020), 59–66.CrossRefGoogle Scholar
Merca, M., ‘On the Ramanujan-type congruences modulo 8 for the overpartitions into odd parts’, Quaest. Math. 45(10) (2022), 1567–1574.CrossRefGoogle Scholar
Munagi, A. O. and Sellers, J. A., ‘Refining overlined parts in overpartitions via residue classes: Bijections, generating functions, and congruences’, Util. Math. 95 (2014), 33–49.Google Scholar
OEIS Foundation Inc., The On-Line Encyclopedia of Integer Sequences (2024), published electronically at https://oeis.org.Google Scholar
Ranganatha, D., ‘On some new congruences for $\ell$ -regular overpartitions’, Palest. J. Math. 7(1) (2018), 345–362.Google Scholar
Ray, C., ‘Divisibility and distribution of $2\ell$ -regular overpartitions’, J. Ramanujan Math. Soc. 36(4) (2021), 331–337.Google Scholar
Ray, C. and Barman, R., ‘Infinite families of congruences for $k$ -regular overpartitions’, Int. J. Number Theory 14(1) (2018), 19–29.CrossRefGoogle Scholar
Saikia, N. and Boruah, C., ‘Congruences for $\ell$ -regular overpartition for $\ell \in \left\{5,6,8\right\}$ ’, Indian J. Pure Appl. Math. 48(2) (2017), 295–308.CrossRefGoogle Scholar
Sellers, J. A., ‘An elementary proof of a conjecture of Saikia on congruences for $t$ -colored overpartitions’, Bol. Soc. Mat. Mex. (3) 30(1) (2024), Article no. 2.Google Scholar
Shen, E. Y. Y., ‘Arithmetic properties of $\ell$ -regular overpartitions’, Int. J. Number Theory 12(3) (2016), 841–852.CrossRefGoogle Scholar
Shivashankar, C. and Gireesh, D. S., ‘Congruences for $\ell$ -regular overpartitions into odd parts’, Bol. Soc. Mat. Mex. (3) 28(1) (2022), Article no. 23.Google Scholar
Tang, D., ‘Congruence properties modulo powers of 2 for overpartitions and overpartition pairs’, Int. J. Number Theory 20(2) (2024), 357–380.CrossRefGoogle Scholar
Xia, E. X. W., ‘Some new infinite families of congruences modulo 3 for overpartitions into odd parts’, Colloq. Math. 142(2) (2016), 255–266.CrossRefGoogle Scholar
Xia, E. X. W., ‘Congruences modulo 9 and 27 for overpartitions’, Ramanujan J. 42(2) (2017), 301–323.CrossRefGoogle Scholar
Yang, X., Cui, S.-P. and Lin, B. L. S., ‘Overpartition function modulo powers of 2’, Ramanujan J. 44(1) (2017), 89–104.CrossRefGoogle Scholar
Yao, O. X. M., ‘Congruences modulo 64 and 1024 for overpartitions’, Ramanujan J. 46(1) (2018), 1–18.CrossRefGoogle Scholar
Yao, O. X. M. and Xia, E. X. W., ‘New Ramanujan-like congruences modulo powers of 2 and 3 for overpartitions’, J. Number Theory 133(6) (2013), 1932–1949.CrossRefGoogle Scholar
Zhang, L., ‘New congruences for overpartitions modulo 3 and 9’, Rocky Mountain J. Math. 51(6) (2021), 2269–2273.CrossRefGoogle Scholar
Zhao, T. Y. and Jin, L. J., ‘New congruences modulo 5 for overpartitions’, Colloq. Math. 145(2) (2016), 285–290.Google Scholar