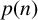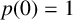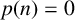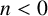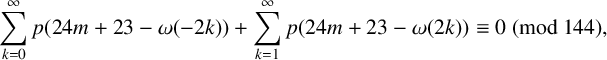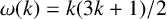Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Biswas, Sabi
and
Saikia, Nipen
2024.
Divisibility of sums of some restricted partition numbers by $${\textbf {2}}$$, $${\textbf {3}}$$ and $${\textbf {4}}$$.
Boletín de la Sociedad Matemática Mexicana,
Vol. 30,
Issue. 2,