Hostname: page-component-669899f699-g7b4s Total loading time: 0 Render date: 2025-04-27T22:38:54.889Z Has data issue: false hasContentIssue false
  • English
  • Français

A CONJECTURE OF ZHI-WEI SUN ON MATRICES CONCERNING MULTIPLICATIVE SUBGROUPS OF FINITE FIELDS

Part of: Algebraic number theory: global fields Basic linear algebra Finite fields and commutative rings (number-theoretic aspects) General field theory

Published online by Cambridge University Press:  27 September 2024

JIE LI Open the ORCID record for JIE LI [Opens in a new window]  and
HAI-LIANG WU Open the ORCID record for HAI-LIANG WU [Opens in a new window]
JIE LI
Affiliation:
School of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, PR China e-mail: [email protected]
HAI-LIANG WU*
Affiliation:
School of Science, Nanjing University of Posts and Telecommunications, Nanjing 210023, PR China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Motivated by the recent work of Zhi-Wei Sun [‘Problems and results on determinants involving Legendre symbols’, Preprint, arXiv:2405.03626], we study some matrices concerning subgroups of finite fields. For example, let 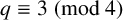$q\equiv 3\pmod 4$ be an odd prime power and let 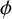$\phi $ be the unique quadratic multiplicative character of the finite field 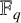$\mathbb {F}_q$. If the set 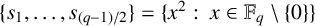$\{s_1,\ldots ,s_{(q-1)/2}\}=\{x^2:\ x\in \mathbb {F}_q\setminus \{0\}\}$, then we prove that

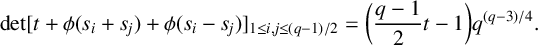$$ \begin{align*}\det[t+\phi(s_i+s_j)+\phi(s_i-s_j)]_{1\le i,j\le (q-1)/2}=\bigg(\frac{q-1}{2}t-1\bigg)q^{{(q-3)}/{4}}.\end{align*} $$

This confirms a conjecture of Zhi-Wei Sun.

Keywords

Legendre symbolsfinite fieldscyclotomic matricesdeterminants

MSC classification

Primary: 11T24: Other character sums and Gauss sums
Secondary: 11R18: Cyclotomic extensions 12E20: Finite fields (field-theoretic aspects) 15A15: Determinants, permanents, other special matrix functions
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , First View , pp. 1 - 7
Check for updates
Copyright
© The Author(s), 2024. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

Footnotes

This work was supported by the Natural Science Foundation of China (Grant No. 12101321).

References

Carlitz, L., ‘Some cyclotomic matrices’, Acta Arith. 5 (1959), 293–308.CrossRefGoogle Scholar
Chapman, R., ‘Determinants of Legendre symbol matrices’, Acta Arith. 115 (2004), 231–244.CrossRefGoogle Scholar
Krachun, D., Petrov, F., Sun, Z.-W. and Vsemirnov, M., ‘On some determinants involving Jacobi symbols’, Finite Fields Appl. 64 (2020), Article no. 101672.CrossRefGoogle Scholar
Lehmer, D. H., ‘On certain character matrices’, Pacific J. Math. 6 (1956), 491–499.CrossRefGoogle Scholar
Sun, Z.-W., ‘On some determinants with Legendre symbols entries’, Finite Fields Appl. 56 (2019), 285–307.CrossRefGoogle Scholar
Sun, Z.-W., ‘Problems and results on determinants involving Legendre symbols’, Preprint, 2024, arXiv:2405.03626.Google Scholar
Wu, H.-L., ‘Elliptic curves over ${F}_p$ and determinants of Legendre matrices’, Finite Fields Appl. 76 (2021), Article no. 101929.CrossRefGoogle Scholar