Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-05-04T04:19:30.084Z Has data issue: false hasContentIssue false
  • English
  • Français

CONGRUENCE OF SYMMETRIC INNER PRODUCTS OVER FINITE COMMUTATIVE RINGS OF ODD CHARACTERISTIC

Part of: Forms and linear algebraic groups Finite commutative rings

Published online by Cambridge University Press:  08 June 2017

SONGPON SRIWONGSA Open the ORCID record for SONGPON SRIWONGSA [Opens in a new window]
SONGPON SRIWONGSA*
Affiliation:
Department of Mathematical Sciences, University of Wisconsin-Milwaukee, WI, 53211, USA email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 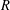$R$ be a finite commutative ring of odd characteristic and let 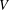$V$ be a free 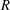$R$-module of finite rank. We classify symmetric inner products defined on 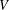$V$ up to congruence and find the number of such symmetric inner products. Additionally, if 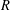$R$ is a finite local ring, the number of congruent symmetric inner products defined on 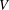$V$ in each congruence class is determined.

Keywords

congruencelocal ringsymmetric inner product

MSC classification

Primary: 11E08: Quadratic forms over local rings and fields
Secondary: 13M99: None of the above, but in this section
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 96 , Issue 3 , December 2017 , pp. 389 - 397
Copyright
© 2017 Australian Mathematical Publishing Association Inc. 

References

Bini, G. and Flamini, F., Finite Commutative Rings and Their Applications (Spinger, New York, 2002).CrossRefGoogle Scholar
Casselman, W., ‘Quadratic forms over finite fields’, 2011,http://www.math.ubc.ca/ cass/siegel/Minkowski.pdf.Google Scholar
MacWilliams, J., ‘Orthogonal matrices over finite fields’, Amer. Math. Monthly 76(2) (1969), 152–164.CrossRefGoogle Scholar
McDonald, B. R., Finite Rings with Identity (Marcel Dekker, New York, 1974).Google Scholar
McDonald, B. R. and Hershberger, B., ‘The orthogonal group over a full ring’, J. Algebra. 51 (1978), 536–549.CrossRefGoogle Scholar