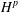Hostname: page-component-669899f699-vbsjw Total loading time: 0 Render date: 2025-04-29T11:05:52.020Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPACT WEIGHTED COMPOSITION OPERATORS ON $H^{p}$-SPACES

Part of: Spaces and algebras of analytic functions Special classes of linear operators

Published online by Cambridge University Press:  26 February 2019

CHING-ON LO Open the ORCID record for CHING-ON LO [Opens in a new window]  and
ANTHONY WAI-KEUNG LOH Open the ORCID record for ANTHONY WAI-KEUNG LOH [Opens in a new window]
CHING-ON LO*
Affiliation:
Division of Science and Technology, Hong Kong Community College, The Hong Kong Polytechnic University, Hong Kong email [email protected]
ANTHONY WAI-KEUNG LOH
Affiliation:
Division of Science and Technology, Hong Kong Community College, The Hong Kong Polytechnic University, Hong Kong email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

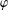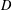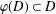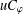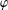Let $u$ and $\unicode[STIX]{x1D711}$ be two analytic functions on the unit disc $D$ such that $\unicode[STIX]{x1D711}(D)\subset D$. A weighted composition operator $uC_{\unicode[STIX]{x1D711}}$ induced by $u$ and $\unicode[STIX]{x1D711}$ is defined by 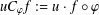$uC_{\unicode[STIX]{x1D711}}f:=u\cdot f\circ \unicode[STIX]{x1D711}$ for every 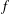$f$ in 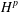$H^{p}$, the Hardy space of 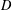$D$. 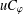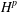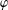We investigate compactness of $uC_{\unicode[STIX]{x1D711}}$ on $H^{p}$ in terms of function-theoretic properties of $u$ and $\unicode[STIX]{x1D711}$.

Keywords

weighted composition operatorsHardy spacescompact operators

MSC classification

Primary: 47B33: Composition operators
Secondary: 30H10: Hardy spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 3 , June 2019 , pp. 473 - 484
Copyright
© 2019 Australian Mathematical Publishing Association Inc. 

References

Contreras, M. D. and Hernández-Díaz, A. G., ‘Weighted composition operators on Hardy spaces’, J. Math. Anal. Appl. 263 (2001), 224–233.Google Scholar
Čučković, Ž. and Zhao, R., ‘Weighted composition operators between different weighted Bergman spaces and different Hardy spaces’, Illinois J. Math. 51 (2007), 479–498.Google Scholar
Gunatillake, G., ‘Compact weighted composition operators on the Hardy space’, Proc. Amer. Math. Soc. 136 (2008), 2895–2899.Google Scholar
Matache, V., ‘Weighted composition operators on H 2 and applications’, Complex Anal. Oper. Theory 2 (2008), 169–197.Google Scholar
Ohno, S. and Takagi, H., ‘Some properties of weighted composition operators on algebras of analytic functions’, J. Nonlinear Convex Anal. 2 (2001), 369–380.Google Scholar
Shapiro, J. H., ‘The essential norm of a composition operator’, Ann. of Math. (2) 125 (1987), 375–404.Google Scholar
Shapiro, J. H., Composition Operators and Classical Function Theory (Springer, New York, 1993).Google Scholar
Smith, W., ‘Composition operators between Bergman and Hardy spaces’, Trans. Amer. Math. Soc. 348 (1996), 2331–2348.Google Scholar