Hostname: page-component-669899f699-b58lm Total loading time: 0 Render date: 2025-04-29T03:40:47.384Z Has data issue: false hasContentIssue false
  • English
  • Français

A CHARACTERISATION OF EUCLIDEAN NORMED PLANES VIA BISECTORS

Part of: General convexity Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  20 August 2018

JAVIER CABELLO SÁNCHEZ  and
ADRIÁN GORDILLO-MERINO
JAVIER CABELLO SÁNCHEZ*
Affiliation:
Departamento de Matemáticas, Universidad de Extremadura, Avda. de Elvas s/n, 06006 Badajoz, Spain email [email protected]
ADRIÁN GORDILLO-MERINO
Affiliation:
Departamento de Matemáticas, Universidad de Extremadura, Avda. de Elvas s/n, 06006 Badajoz, Spain email [email protected]
*
✉[email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Our main result states that whenever we have a non-Euclidean norm 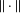$\Vert \cdot \Vert$ on a two-dimensional vector space 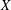$X$, there exists some 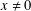$x\neq 0$ such that for every 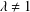$\unicode[STIX]{x1D706}\neq 1$, 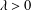$\unicode[STIX]{x1D706}>0$, there exist 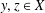$y,z\in X$ satisfying 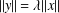$\Vert y\Vert =\unicode[STIX]{x1D706}\Vert x\Vert$, 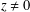$z\neq 0$ and $z$ belongs to the bisectors 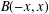$B(-x,x)$ and 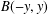$B(-y,y)$. We also give several results about the geometry of the unit sphere of strictly convex planes.

Keywords

isosceles orthogonalitystrictly convex normed spacesEuclidean planesbisectors

MSC classification

Primary: 46B20: Geometry and structure of normed linear spaces
Secondary: 52A10: Convex sets in $2$ dimensions (including convex curves) 52A21: Finite-dimensional Banach spaces (including special norms, zonoids, etc.)
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 99 , Issue 1 , February 2019 , pp. 121 - 129
Copyright
© 2018 Australian Mathematical Publishing Association Inc. 

Footnotes

The first author was supported in part by DGICYT project MTM2016⋅76958⋅C2⋅1⋅P (Spain) and Junta de Extremadura programs GR⋅15152 and IB⋅16056; the second author was partially supported by Junta de Extremadura and FEDER funds.

References

Alonso, J., ‘Uniqueness properties of isosceles orthogonality in normed linear spaces’, Ann. Sci. Math. Québec 18(1) (1994), 25–38.Google Scholar
Alonso, J., Martini, H. and Wu, S., ‘On Birkhoff orthogonality and isosceles orthogonality in normed linear spaces’, Aequationes Math. 83(1–2) (2012), 153–189.Google Scholar
Bárány, I. and Schneider, R., ‘Universal points of convex bodies and bisectors in Minkowski spaces’, Adv. Geom. 14(3) (2014), 427–445.Google Scholar
He, C., Martini, H. and Wu, S., ‘On bisectors for convex distance functions’, Extracta Math. 28(1) (2013), 23–30.Google Scholar
Jahn, T. and Spirova, M., ‘On bisectors in normed planes’, Contrib. Discrete Math. 10(2) (2018), 1–9.Google Scholar
James, R. C., ‘Orthogonality in normed linear spaces’, Duke Math. J. 12(2) (1945), 291–302.Google Scholar
Ji, D., Li, J. and Wu, S., ‘On the uniqueness of isosceles orthogonality in normed linear spaces’, Results Math. 59(1) (2011), 157–162.Google Scholar
Ma, L., Bisectors and Voronoi Diagrams for Convex Distance Functions, PhD Thesis, Fachbereich Informatik, Fernuniversität Hagen, 2000.Google Scholar
Martini, H. and Swanepoel, K. J., ‘The geometry of Minkowski spaces—a survey. Part II’, Expo. Math. 22(2) (2004), 93–144.Google Scholar
Thomson, A. C., Minkowski Geometry (Cambridge University Press, Cambridge, 1996).Google Scholar